题目内容
9.某人要在规定时间内骑车到达某地,若每小时行15千米,则可早到15分钟;若每小时行9千米,则要迟到15分钟.现打算提前10分钟到达,问:此人骑车速度应为多少千米/小时?分析 利用已知首先结合规定时间不变得出等式,进而求出总的路程,进而得出求出规定的时间即可得出打算提前10分钟到达时的速度.
解答 解:设此人骑车速度应为x千米/小时,总路程为akm,根据题意可得:
$\frac{a}{15}$+$\frac{15}{60}$=$\frac{a}{9}$-$\frac{15}{60}$,
解得:a=$\frac{45}{4}$,
则规定时间是:$\frac{\frac{45}{4}}{15}$+$\frac{15}{60}$=1(小时),
故$\frac{\frac{45}{4}}{x}$+$\frac{10}{60}$=1,
解得:x=$\frac{27}{2}$=13.5,
检验得:x=13.5是原方程的根.
答:此人骑车速度应为多13.5千米/小时.
点评 此题主要考查了一元一次方程的应用,根据题意得出总路程和规定时间是解题关键.

练习册系列答案
相关题目
19.规定:在平面内,将一个图形绕着某一点旋转一定的角度(小于周角)后能和自身重合,就称此图形为旋转对称图形,那么下列图形中是旋转对称图形,且有一个旋转角为60°的是( )
| A. | 正八边形 | B. | 正六边形 | C. | 正方形 | D. | 正三角形 |
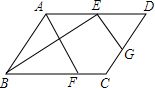 如图,在?ABCD中,点E,F,G分别是AD,BC,CD的中点,BE⊥EG,AD=2$\sqrt{5}$,AB=3,求AF的长.
如图,在?ABCD中,点E,F,G分别是AD,BC,CD的中点,BE⊥EG,AD=2$\sqrt{5}$,AB=3,求AF的长.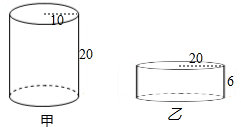 如图所示,有甲、乙两个容器,甲容器盛满了水,乙容器里没有水,现将甲容器中的水全部倒入乙容器,问:乙容器的水会不会溢出?如果不会溢出,请你求出倒入水后乙容器的水深;如果水会溢出,请你说明理由.(图中数据的单位:cm)
如图所示,有甲、乙两个容器,甲容器盛满了水,乙容器里没有水,现将甲容器中的水全部倒入乙容器,问:乙容器的水会不会溢出?如果不会溢出,请你求出倒入水后乙容器的水深;如果水会溢出,请你说明理由.(图中数据的单位:cm)