题目内容
已知:关于x的一元二次方程:x2-2mx+m2-4=0.
(1)求证:这个方程有两个不相等的实数根;
(2)当抛物线y=x2-2mx+m2-4与x轴的交点位于原点的两侧,且到原点的距离相等时,求此抛物线的解析式.
(1)证明:∵Δ=(-2m)2-4(m2-4)=16>0.
∴该方程总有两个不相等的实数根.
(2)由题意可知y轴是抛物线的对称轴,
∴- =0,解得m=0.
=0,解得m=0.
∴此抛物线的解析式为y=x2-4.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
 图4236
图4236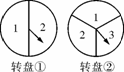
 ,0,
,0, ,0.2
,0.2 ,cos60°,
,cos60°, ,0.030 030 003…,1-
,0.030 030 003…,1- 中,无理数有( )
中,无理数有( ) 
