题目内容
15.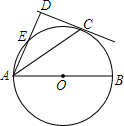 己知:AB是⊙O的直径,点E,C是⊙O上的两点,AC平分∠BAD,AD⊥CD.若CD=8,DE=4,求⊙O的半径.
己知:AB是⊙O的直径,点E,C是⊙O上的两点,AC平分∠BAD,AD⊥CD.若CD=8,DE=4,求⊙O的半径.
分析 连接OC,BC,推出∠DAC=∠OCA=∠CAO,推出OC∥AD,推出OC⊥DF,根据切线判定证出CD是⊙O的切线,由切线长定理求出AD,由勾股定理求出AC,证△DAC∽△CAB,得出比例式,求出AB,即可得出⊙O的半径.
解答 解:连接OCBC,如图所示: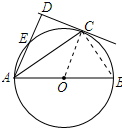
∵OA=OC,
∴∠OAC=∠OCA,
∵AC平分∠BAD,
∴∠DAC=∠OAC,
∴∠DAC=∠OCA,
∴AD∥OC,
∴∠ADC=∠OCF,
∵AD⊥DC,
∴∠ADC=90°,
∴∠OCF=90°,
∴OC⊥CD,
∵OC为半径,
∴CD是⊙O的切线,
∴CD2=DE•DA,即82=4×DA,
∴DA=16,
∴AC=$\sqrt{C{D}^{2}+D{A}^{2}}$=8$\sqrt{5}$,
∵AB是直径,
∴∠ACB=90°=∠ADC,
∵∠DAC=∠BAC,
∴△ADC∽△ACB,
∴$\frac{AC}{AB}=\frac{AD}{AC}$,即$\frac{8\sqrt{5}}{AB}=\frac{16}{8\sqrt{5}}$,
解得:AB=20,
∴OA=10,
即⊙O的半径为10.
点评 本题考查了相似三角形的性质和判定,勾股定理,圆周角定理,平行线性质和判定,等腰三角形性质,切线长定理等知识;本题综合性强,证明CD是⊙O的切线是解决问题的关键.

练习册系列答案
相关题目
5.一次体检中,某班学生视力结果如下表:
从表中看出全班视力数据的众数是1.0.
| 0.7以下 | 0.7 | 0.8 | 0.9 | 1.0 | 1.0以上 |
| 5% | 8% | 15% | 20% | 40% | 12% |
6.某运动队欲从甲、乙两名优秀选手中选一名参加全省射击比赛,该运动队预先对这两名选手进行了8次测试,测得的成绩如表:
根据统计的测试成绩,请你运用所学过的统计知识作出判断,派哪一位选手参加比赛更好?为什么?
| 次数 | 选手甲的成绩(环) | 选手乙的成绩(环) |
| 1 | 9.6 | 9.5 |
| 2 | 9.7 | 9.9 |
| 3 | 10.5 | 10.3 |
| 4 | 10.0 | 9.7 |
| 5 | 9.7 | 10.5 |
| 6 | 9.9 | 10.3 |
| 7 | 10.0 | 10.0 |
| 8 | 10.6 | 9.8 |
7. 如图所示,不能判定△ABC∽△DAC的条件是( )
如图所示,不能判定△ABC∽△DAC的条件是( )
 如图所示,不能判定△ABC∽△DAC的条件是( )
如图所示,不能判定△ABC∽△DAC的条件是( )| A. | ∠B=∠DAC | B. | ∠BAC=∠ADC | C. | AD2=BD•BC | D. | AC2=DC•BC |
 如图,点C、D在线段AB上,△PCD是等边三角形,且△ACP∽△PDB,求∠APB的度数.
如图,点C、D在线段AB上,△PCD是等边三角形,且△ACP∽△PDB,求∠APB的度数.



 如图,已知平面内两点A,B.
如图,已知平面内两点A,B.