题目内容
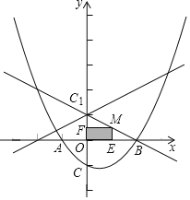
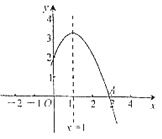
【题目】如图所示，二次函数
（
，
，
是常数，
）的图象的一部分与
轴的交点
在
与
之间，对称轴为直线
.下列结论：①
；②
；③
；④
（
为实数）；⑤当
时，
.其中，正确结论的个数是（ ）
A. 2B. 3C. 4D. 5
【答案】B
【解析】
由抛物线的开口方向判断a与0的关系，然后根据对称轴判定b与0的关系以及2a+b=0；当x=-1时，y=a-b+c；然后由图象确定当x取何值时，y＞0．
解：①∵对称轴在y轴右侧，
∴a、b异号，
∴ab＜0，故①正确；
②∵对称轴x=1，
∴-
2a+b=0；故②正确；
③∵2a+b=0，
∴b=-2a，
∵当x=-1时，y=a-b+c＜0，
∴a-（-2a）+c=3a+c＜0，故③错误；
④∵对称轴x=1，开口向下
∴当x=1时，y有最大值且最大值为a+b+c；
∵
为实数
∴a+b+c
．
∴
故④正确．
⑤如图，当-1＜x＜3时，y不只是大于0．故⑤错误．
故选：B．
激活思维优加课堂系列答案
活力试卷系列答案
【题目】体育组为了了解九年级450名学生排球垫球的情况，随机抽查了九年级部分学生进行排球垫球测试（单位：个），根据测试结果，制成了下面不完整的统计图表：
组别 | 个数段 | 频数 | 频率 |
1 |
| 5 | 0.1 |
2 |
| 21 | 0.42 |
3 |
|
| |
4 |
|
|
（1）表中的数
，
；
（2）估算该九年级排球垫球测试结果小于10的人数；
（3）排球垫球测试结果小于10的为不达标，若不达标的5人中有3个男生，2个女生，现从这5人中随机选出2人调查，试通过画树状图或列表的方法求选出的2人为一个男生一个女生的概率．
【题目】某教学网站策划了
、
两种上网学习的月收费方式：
收费方式 | 月使用费/元 | 月包时上网时间/ | 月超时费/（元/ |
| 7 | 25 | 0.6 |
| 10 | 50 | 3 |
设每月上网学习的时间为
.
（Ⅰ）根据题意，填写下表：
月使用费/元 | 月上网时间/ | 月超时费/元 | 月总费用/元 | |
方式 | 7 | 45 | ||
方式 | 10 | 45 |
（Ⅱ）设，两种方式的收费金额分别为
元和
元，分别写出，与
的函数解析式；
（Ⅲ）当
时，你认为哪种收费方式省钱？请说明理由.
【题目】某山区不仅有美丽风光，也有许多令人喜爱的土特产，为实现脱贫奔小康，某村组织村民加工包装土特产销售给游客，以增加村民收入.已知某种士特产每袋成本10元.试销阶段每袋的销售价x（元）与该士特产的日销售量y（袋）之间的关系如表：
x（元） | 15 | 20 | 30 | … |
y（袋） | 25 | 20 | 10 | … |
若日销售量y是销售价x的一次函数，试求：
（1）日销售量y（袋）与销售价x（元）的函数关系式；
（2）假设后续销售情况与试销阶段效果相同，要使这种土特产每日销售的利润最大，每袋的销售价应定为多少元？每日销售的最大利润是多少元？
