题目内容
10. 如图:AB⊥BC,DC⊥BC,E在BC上,AB=EC,BE=CD,EF⊥AD于F,求证:F是AD中点.
如图:AB⊥BC,DC⊥BC,E在BC上,AB=EC,BE=CD,EF⊥AD于F,求证:F是AD中点.
分析 由已知AB⊥BC,DC⊥BC,AB=EC,BE=CD,根据SAS可得△ABE≌△ECD,根据全等三角形的性质得AE=DE,再根据等腰三角形的三线合一性质即可证明.
解答 解:∵AB⊥BC,DC⊥BC,
∴∠ABE=∠ECD,
在△ABE与△ECD中,
$\left\{\begin{array}{l}{AB=EC}\\{∠ABE=∠ECD}\\{BE=CD}\end{array}\right.$,
∴△ABE≌△ECD,
∴AE=DE,
∵EF⊥AD,
∴F是AD中点.
点评 考查了全等三角形的判定与性质,本题通过三角形全等的判定及性质,推出等腰三角形,再利用等腰三角形的三线合一性质证明线段相等,此证法是比较常用的作法,学生应该掌握.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.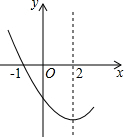 如图是抛物线y=ax2+bx+c(a≠0)图象的一部分.当y<0时,自变量x的范围是( )
如图是抛物线y=ax2+bx+c(a≠0)图象的一部分.当y<0时,自变量x的范围是( )
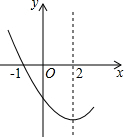 如图是抛物线y=ax2+bx+c(a≠0)图象的一部分.当y<0时,自变量x的范围是( )
如图是抛物线y=ax2+bx+c(a≠0)图象的一部分.当y<0时,自变量x的范围是( )| A. | x<-1或x>2 | B. | x<-1或x>5 | C. | -1<x<5 | D. | -1<x<2 |
19.方程(x-a)(x+b)=0的两根是( )
| A. | x1=a,x2=b | B. | x1=a,x2=-b | C. | x1=-a,x2=b | D. | x1=-a,x2=-b |
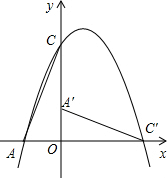 如图,在直角坐标系中,O是坐标原点,点C的坐标是(0,3),抛物线y=-x2+2x+c经过点C,交x轴负半轴于点A.
如图,在直角坐标系中,O是坐标原点,点C的坐标是(0,3),抛物线y=-x2+2x+c经过点C,交x轴负半轴于点A.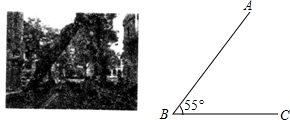 如图,倾斜的大树与地面的夹角∠ABC为55°,高为3.5米的大客车靠近此树的一侧至少要离此树的根部B点多少米才能安全通过?(结果精确到0.1米)
如图,倾斜的大树与地面的夹角∠ABC为55°,高为3.5米的大客车靠近此树的一侧至少要离此树的根部B点多少米才能安全通过?(结果精确到0.1米)