Question

【题目】如图，△ABC中，AB=BC，BD⊥AC于点D，∠FAC=∠ABC，且∠FAC在AC下方．点P，Q分别是射线BD，射线AF上的动点，且点P不与点B重合，点Q不与点A重合，连接CQ，过点P作PE⊥CQ于点E，连接DE．

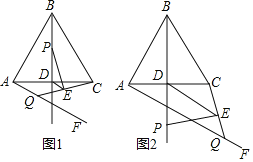
（1）若∠ABC=60°，BP=AQ．

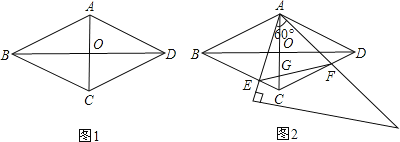
①如图1，当点P在线段BD上运动时，请直接写出线段DE和线段AQ的数量关系和位置关系；

②如图2，当点P运动到线段BD的延长线上时，试判断①中的结论是否成立，并说明理由；

（2）若∠ABC=2α≠60°，请直接写出当线段BP和线段AQ满足什么数量关系时，能使（1）中①的结论仍然成立（用含α的三角函数表示）．

Answer 1

【答案】（1）①DE=AQ，DE∥AQ，理由见解析；② E∥AQ，DE=AQ，理由见解析；（2）AQ=2BPsinα，理由见解析.

【解析】

（1）①先判断出△ABC是等边三角形，进而判断出∠CBP=∠CAQ，即可判断出△BPC≌△AQC，再判断出△PCQ是等边三角形，进而得出CE=QE，即可得出结论；

②同①的方法即可得出结论；

（2）先判断出，∠PAQ=90°﹣∠ACQ，∠BAP=90°﹣∠ACQ，进而得出∠BCP=∠ACQ，即可判断出进而判断出△BPC∽△AQC，最后用锐角三角函数即可得出结论．

（1）①DE=AQ，DE∥AQ，

理由：如图1，连接PC，PQ，

在△ABC中，AB=AC，∠ABC=60°，

∴△ABC是等边三角形，

∴∠ACB=60°，AC=BC，

∵AB=BC，BD⊥AC，

∴AD=CD，∠ABD=∠CBD=∠BAC，

∵∠CAF=∠ABC，

∴∠CBP=∠CAQ，

在△BPC和△AQC中，，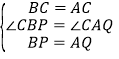

∴△BPC≌△AQC（SAS），

∴PC=QC，∠BPC=∠ACQ，

∴∠PCQ=∠PCA+∠AQC=∠PCA+∠BCP=∠ACB=60°，

∴△PCQ是等边三角形，

∵PE⊥CQ，

∴CE=QE，

∵AD=CD，

∴DE=AQ，DE∥AQ；

②DE∥AQ，DE=AQ，

理由：如图2，连接PQ，PC，

同①的方法得出DE∥AQ，DE=AQ；

（2）AQ=2BPsinα，

理由：连接PQ，PC，

要使DE=AQ，DE∥AQ，

∵AD=CD，

∴CE=QE，

∵PE⊥CQ，

∴PQ=PC，

易知，PA=PC，

∴PA=PE=PC

∴以点P为圆心，PA为半径的圆必过A，Q，C，

∴∠APQ=2∠ACQ，

∵PA=PQ，

∴∠PAQ=∠PQA=（180°﹣∠APQ）=90°﹣∠ACQ，

∵∠CAF=∠ABD，∠ABD+∠BAD=90°，

∴∠BAQ=90°，

∴∠BAP=90°﹣∠PAQ=90°﹣∠ACQ，

易知，∠BCP=∠BAP，

∴∠BCP=∠ACQ，

∵∠CBP=∠CAQ，

∴△BPC∽△AQC，

∴，

在Rt△BCD中，sinα=，

∴=2×=2sinα，

∴AQ=2BPsinα．