题目内容
15.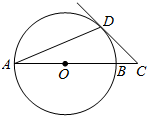 如图,AB是⊙O的直径,AD是弦,∠DAB=22.5°,延长AB到点C,使得∠ACD=45°,
如图,AB是⊙O的直径,AD是弦,∠DAB=22.5°,延长AB到点C,使得∠ACD=45°,求证:CD是⊙O的切线.
分析 连接OD,可求得∠DOC=45°,可证得OD⊥CD,则可得出结论.
解答  证明:
证明:
如图,连接OD,
∵∠DAB=22.5°,
∴∠DOC=2∠DAB=45°,
∵∠ACD=45°,
∴∠ODC=90°,即OD⊥CD,且点D在⊙O上,
∴CD是⊙O的切线.
点评 本题主要考查切线的判定,掌握切线的判定方法是解题的关键.

练习册系列答案
相关题目
6.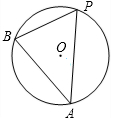 如图,⊙O为△ABP的外接圆,若⊙O的半径为2,∠P=75°,则$\widehat{AB}$的长为( )
如图,⊙O为△ABP的外接圆,若⊙O的半径为2,∠P=75°,则$\widehat{AB}$的长为( )
 如图,⊙O为△ABP的外接圆,若⊙O的半径为2,∠P=75°,则$\widehat{AB}$的长为( )
如图,⊙O为△ABP的外接圆,若⊙O的半径为2,∠P=75°,则$\widehat{AB}$的长为( )| A. | $\frac{5}{12}$π | B. | π | C. | $\frac{5}{3}$π | D. | 2π |
10.一块长方形菜地的面积是150m2,如果它的长减少5m,那么菜地就变成正方形,求原菜地的长和宽.若设长方形的宽为xm,则可得方程为( )
| A. | x(x+5)=150 | B. | x(x-5)=150 | C. | (x+5)(x-5)=150 | D. | (x+5)2=150 |
4. 实数a,b在数轴上的对应点的位置如图所示,把a,-b,0按照从小到大的顺序排列,正确的是( )
实数a,b在数轴上的对应点的位置如图所示,把a,-b,0按照从小到大的顺序排列,正确的是( )
 实数a,b在数轴上的对应点的位置如图所示,把a,-b,0按照从小到大的顺序排列,正确的是( )
实数a,b在数轴上的对应点的位置如图所示,把a,-b,0按照从小到大的顺序排列,正确的是( )| A. | a<0<-b | B. | 0<a<-b | C. | -b<0<a | D. | -b<a<0 |
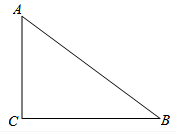 如图,已知Rt△ABC中,∠ACB=90°.请完成以下任务.
如图,已知Rt△ABC中,∠ACB=90°.请完成以下任务.
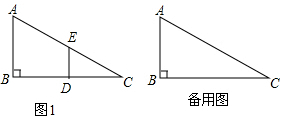 如图1,在Rt△ABC中,∠B=90°,BC=2AB=8,点D、E分别是边BC、AC的中点,连接DE,将△EDC绕点C按顺时针方向旋转,记旋转角为α.
如图1,在Rt△ABC中,∠B=90°,BC=2AB=8,点D、E分别是边BC、AC的中点,连接DE,将△EDC绕点C按顺时针方向旋转,记旋转角为α.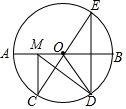 如图,在⊙O中,AB是⊙O的直径,AB=10,$\widehat{AC}$=$\widehat{CD}$=$\widehat{DB}$,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①∠BOE=60°;②∠CED=$\frac{1}{2}$∠DOB;③DM⊥CE;④CM+DM的最小值是10,上述结论中正确的个数是( )
如图,在⊙O中,AB是⊙O的直径,AB=10,$\widehat{AC}$=$\widehat{CD}$=$\widehat{DB}$,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①∠BOE=60°;②∠CED=$\frac{1}{2}$∠DOB;③DM⊥CE;④CM+DM的最小值是10,上述结论中正确的个数是( )