题目内容
5.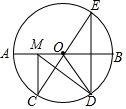 如图,在⊙O中,AB是⊙O的直径,AB=10,$\widehat{AC}$=$\widehat{CD}$=$\widehat{DB}$,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①∠BOE=60°;②∠CED=$\frac{1}{2}$∠DOB;③DM⊥CE;④CM+DM的最小值是10,上述结论中正确的个数是( )
如图,在⊙O中,AB是⊙O的直径,AB=10,$\widehat{AC}$=$\widehat{CD}$=$\widehat{DB}$,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①∠BOE=60°;②∠CED=$\frac{1}{2}$∠DOB;③DM⊥CE;④CM+DM的最小值是10,上述结论中正确的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据$\widehat{AC}$=$\widehat{CD}$=$\widehat{DB}$和点E是点D关于AB的对称点,求出∠DOB=∠COD=∠BOE=60°,求出∠CED,即可判断①②;根据圆周角定理求出当M和A重合时∠MDE=60°
即可判断③;求出M点的位置,根据圆周角定理得出此时DF是直径,即可求出DF长,即可判断④.
解答 解:∵$\widehat{AC}$=$\widehat{CD}$=$\widehat{DB}$,点E是点D关于AB的对称点,
∴$\widehat{BD}$=$\widehat{BE}$,
∴∠DOB=∠BOE=∠COD=$\frac{1}{3}×180°$=60°,∴①正确;
∠CED=$\frac{1}{2}$∠COD=$\frac{1}{2}×60°$=30°=$\frac{1}{2}∠DOB$,∴②正确;
∵$\widehat{BE}$的度数是60°,
∴$\widehat{AE}$的度数是120°,
∴只有当M和A重合时,∠MDE=60°,
∵∠CED=30°,
∴只有M和A重合时,DM⊥CE,∴③错误;
做C关于AB的对称点F,连接CF,交AB于N,连接DF交AB于M,此时CM+DM的值最短,等于DF长,
连接CD,
∵$\widehat{AC}$=$\widehat{CD}$=$\widehat{DB}$=$\widehat{AF}$,并且弧的度数都是60°,
∴∠D=$\frac{1}{2}×120°$=60°,∠CFD=$\frac{1}{2}×60°$=30°,
∴∠FCD=180°-60°-30°=90°,
∴DF是⊙O的直径,
即DF=AB=10,
∴CM+DM的最小值是10,∴④正确;
故选C.
点评 本题考查了圆周角定理,轴对称-最短问题等知识点,能灵活运用圆周角定理求出各个角的度数和求出M的位置是解此题的关键.

 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 七 |
| 增减(单位:个) | +5 | -2 | -5 | +15 | -10 | +16 | -9 |
(2)本周产量中最多的一天比最少的一天多生产26个工艺品;
(3)求该工艺厂在本周实际生产工艺品多少个?
(4)已知该厂实际每日计件工资制,每生产一个工艺品可得60元,若超额完成任务,则超过部分每个另奖50元,少生产一个扣80元,求该工艺厂在这一周应付出的工资总额是多少元?
| A. | 正五边形 | B. | 平行四边形 | C. | 矩形 | D. | 等边三角形 |
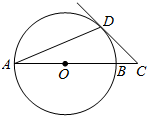 如图,AB是⊙O的直径,AD是弦,∠DAB=22.5°,延长AB到点C,使得∠ACD=45°,
如图,AB是⊙O的直径,AD是弦,∠DAB=22.5°,延长AB到点C,使得∠ACD=45°,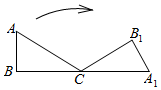 如图,在Rt△ABC中,∠A=60°,AB=1,将Rt△ABC绕点C按顺时针方向旋转到△A1B1C的位置,点A1刚好落在BC的延长线上,求点A从开始到结束所经过的路径长为(结果保留π)$\frac{5}{3}$π.
如图,在Rt△ABC中,∠A=60°,AB=1,将Rt△ABC绕点C按顺时针方向旋转到△A1B1C的位置,点A1刚好落在BC的延长线上,求点A从开始到结束所经过的路径长为(结果保留π)$\frac{5}{3}$π.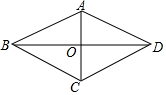 如图,在四边形ABCD中,AB=AD,BD平分∠ABC,AC⊥BD,垂足为点O.
如图,在四边形ABCD中,AB=AD,BD平分∠ABC,AC⊥BD,垂足为点O.