题目内容
15. 如图,在菱形ABCD和菱形BEFG中,点A、B、E在同一直线上,P是线段DF的中点,连接PG、PC.若∠ABC=∠BEF=60°,则$\frac{PG}{CG}$的值为$\frac{\sqrt{3}}{2}$.
如图,在菱形ABCD和菱形BEFG中,点A、B、E在同一直线上,P是线段DF的中点,连接PG、PC.若∠ABC=∠BEF=60°,则$\frac{PG}{CG}$的值为$\frac{\sqrt{3}}{2}$.
分析 可通过构建全等三角形求解.延长GP交DC于H,可证三角形DHP和PGF全等,已知的有DC∥GF,根据平行线间的内错角相等可得出两三角形中两组对应的角相等,又有DP=PF,因此构成了全等三角形判定条件中的(ASA),于是两三角形全等,那么HP=PG,可根据三角函数来得出PG、CG的比例关系.
解答 解:如图,
延长GP交DC于点H,
∵P是线段DF的中点,
∴FP=DP,
由题意可知DC∥GF,
∴∠GFP=∠HDP,
在△GFP和△HDP中
$\left\{\begin{array}{l}{∠GPF=∠HPD}\\{PF=DP}\\{∠GFP=∠HDP}\end{array}\right.$,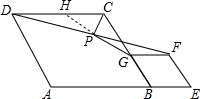
∴△GFP≌△HDP(ASA),
∴GP=HP,GF=HD,
∵四边形ABCD是菱形,
∴CD=CB,
∴CG=CH,
∴△CHG是等腰三角形,
∴PG⊥PC,(三线合一)
又∵∠ABC=∠BEF=60°,
∴∠GCP=60°,
∴$\frac{PG}{CG}$=sin60°=$\frac{\sqrt{3}}{2}$;
故答案为:$\frac{\sqrt{3}}{2}$.
点评 本题主要考查了菱形的性质,以及全等三角形的判定等知识点,根据已知和所求的条件正确的构建出相关的全等三角形是解题的关键.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
6.已知圆周率π=3.1415926…,将π精确到千分位的结果是( )
| A. | 3.1 | B. | 3.14 | C. | 3.141 | D. | 3.142 |
10.已知一次函数y=ax+b(a、b为常数且a≠0)经过(1,3)和(0,-2),求a-b的值( )
| A. | -1 | B. | -3 | C. | 3 | D. | 7 |
20.若x=2,y=-1,那么代数式x2+2xy+y2的值是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 4. |