题目内容
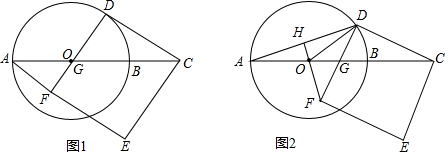
13.如图,AB是⊙O的直径,点C在AB的延长线上,且BC=BO,D是⊙O上一动点且在AB的上方,以CD为边在CD的下方作正方形CDFE,DF和直径AB交于点O,连接FO,DO,AD,延长FO交AD于H.(1)如图1,当DF经过O时,求∠ACD的度数;
(2)如图2,若点G恰好是OB的中点,①求证:△OGD∽△ODC;②求tan∠DAB的值.
分析 (1)在Rt△ODC中,求出∠ACD的值即可解决问题.
(2)①设OG=GB=a,则OB=BC=OD=2a,可知OD2=OG•OC=4a2,推出$\frac{OD}{OG}$=$\frac{OC}{OD}$,由∠DOG=∠COD,即可证明△DOG∽△COD.
②连接BD,作GM⊥AD于M,GN⊥DB于N.只要证明∠BDG=∠CDB=∠ADG,由GM⊥AD,GN⊥DB,推出GM=GN,可知S△ADG:S△DGB=$\frac{1}{2}$AD•GM:$\frac{1}{2}$•DB•GN=AD+DB=AG:GB=3:1,推出tan∠DAC=$\frac{DB}{AD}$=$\frac{1}{3}$即可.
解答 (1)解:如图1中,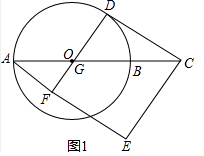
∵四边形EFDC是正方形,
∴∠ODC=90°,
∵OB=BC=OD,
∴OC=2OD,
∴sin∠ACD=$\frac{OD}{OC}$=$\frac{1}{2}$,
∴∠ACD=30°.
(2)解:如图2中,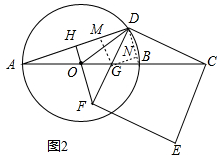
①证明:设OG=GB=a,则OB=BC=OD=2a,
∴OD2=OG•OC=4a2,
∴$\frac{OD}{OG}$=$\frac{OC}{OD}$,∵∠DOG=∠COD,
∴△DOG∽△COD.
②连接BD,作GM⊥AD于M,GN⊥DB于N.
∵AB是直径,
∴∠ADB=∠GDC=90°,
∴∠ADG=∠CDB,
∵△DOG∽△COD,
∴∠ODG=∠DCB,
∵OD=OB,
∴∠ODB=∠OBD,
∴∠ODG+∠BDG=∠BDC+∠DCB,
∴∠BDG=∠CDB=∠ADG,
∵GM⊥AD,GN⊥DB,
∴GM=GN,
∵S△ADG:S△DGB=$\frac{1}{2}$AD•GM:$\frac{1}{2}$•DB•GN=AD+DB=AG:GB=3:1,
∴$\frac{DB}{AD}$=$\frac{1}{3}$,
∴tan∠DAC=$\frac{DB}{AD}$=$\frac{1}{3}$.
点评 本题考查相似三角形的判定和性质、正方形的性质、解直角三角形、圆周角定理、勾股定理等知识,解题的关键是学会利用参数解决问题,本题体现了数形结合的数学思想,学会添加常用辅助线,掌握用面积法证明线段之间的关系,属于中考压轴题.

 一本好题口算题卡系列答案
一本好题口算题卡系列答案| A. |  | B. |  | C. |  | D. |  |
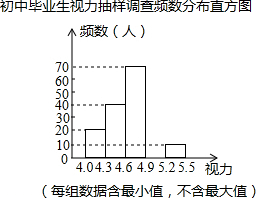 某区对即将参加中考的5000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和不完整的频数分布直方图,请根据图表信息回答下列问题:
某区对即将参加中考的5000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和不完整的频数分布直方图,请根据图表信息回答下列问题:初中毕业生视力抽样调查频数分布表
| 视力 | 频数(人) | 频率 |
| 4.0≤x<4.3 | 20 | 0.1 |
| 4.3≤x<4.6 | 40 | 0.2 |
| 4.6≤x<4.9 | 70 | 0.35 |
| 4.9≤x<5.2 | a | 0.3 |
| 5.2≤x<5.5 | 10 | b |
(2)在频数分布表中,a=60,b=0.05,并将频数分布直方图补充完整;
(3)若视力在4.6以上(含4.6)均属正常,根据上述信息估计全区初中毕业生中视力正常的学生有多少人?
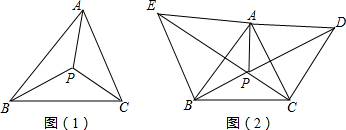
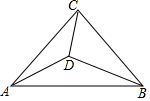 如图,在等腰直角△ABC中,∠ACB=90°,点D为三角形内一点,且∠ACD=∠DAB=∠DBC.
如图,在等腰直角△ABC中,∠ACB=90°,点D为三角形内一点,且∠ACD=∠DAB=∠DBC.