题目内容
如图,A、B两点分别在x轴和y轴上,且OA=OB=
,动点P、Q分别在AB、OB上运动,运动时,始终保持∠OPQ=45°不变,设PA=x,OQ=y.
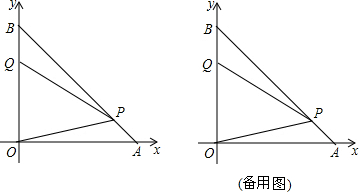
(1)求y与x的函数关系式.
(2)已知点M在坐标平面内,是否存在以P、Q、O、M为顶点的四边形是菱形?若存在,求出点M的坐标;若不存在,说明理由.
(3)已知点D在AB上,且AD=
,试探究:当点P从点A出发第一次运动到点D时,点Q运动的路径长为多少?
| 2 |

(1)求y与x的函数关系式.
(2)已知点M在坐标平面内,是否存在以P、Q、O、M为顶点的四边形是菱形?若存在,求出点M的坐标;若不存在,说明理由.
(3)已知点D在AB上,且AD=
| 3 |
| 2 |
考点:一次函数综合题
专题:综合题,压轴题
分析:(1)利用外角的知识先得出∠APO=∠BQP,继而得出△BQP∽△APO,然后利用对应边成比例可得出y与x的函数关系式;
(2)根据菱形的性质可得,可确定Q的坐标,再由菱形的性质即可确定M的坐标;
(3)根据(1)的函数关系式,即可得出点Q运动的路径长.
(2)根据菱形的性质可得,可确定Q的坐标,再由菱形的性质即可确定M的坐标;
(3)根据(1)的函数关系式,即可得出点Q运动的路径长.
解答:解:(1)∵OA=OB=
,
∴AB=2,
∵OQ=y,
∴BQ=
-y,
∵∠APO=∠PBO+∠BOP=45°+∠BOP,∠BQP=∠BOP+∠OPQ=45°+∠BOP,
∴∠APO=∠BQP,
又∵∠A=∠B=45°,
∴△BQP∽△APO,
∴
=
,即
=
,
∴y=
x2-
x+
.
(2)∵以P、Q、O、M为顶点的四边形是菱形,
当OP是菱形的对角线时,则PQ=OQ,
∵∠OPQ=45°,
∴∠OPQ=∠QOP=45°,
∴∠PQO=90°,
故可得点Q在OB中点处,
如图所示:

此时点M的坐标为(
,0);
当OP是菱形的一边时,
①若OQ=OP,如图所示:

此时点M的坐标为(
,
);
②若OM=OP,
如图所示:

此时△BQP≌△APO,则BP=OA=
,AP=AB-BP=2-
,
过点P作PE⊥x轴于点E,
在等腰直角△APE中,PE=
=
-1,AE=
-1,OE=OA-AE=1,
∵四边形MOPQ为菱形,
∴点M与点P关于y轴对称,
∴点M的坐标为(-1,
-1);
综上可得点M的坐标为:(
,0)或(
,
)或(-1,
-1);
(3)如图所示:

点P运动 的3个界点位置分别是x=0,1,
,
当点P在点A处时,x1=0时,y1=
,
当点P在P1处时,x2=1时,y2=
,
故BQ2=y1-y2=
-
=
,
当点P位于点P3时,x3=
时,y3=
,
故Q2Q3=y3-y2=
,
点Q运动的路径长=BQ2+Q2Q3=
+
=
.
| 2 |
∴AB=2,
∵OQ=y,
∴BQ=
| 2 |
∵∠APO=∠PBO+∠BOP=45°+∠BOP,∠BQP=∠BOP+∠OPQ=45°+∠BOP,
∴∠APO=∠BQP,
又∵∠A=∠B=45°,
∴△BQP∽△APO,
∴
| BQ |
| AP |
| BP |
| AO |
| ||
| x |
| 2-x | ||
|
∴y=
| ||
| 2 |
| 2 |
| 2 |
(2)∵以P、Q、O、M为顶点的四边形是菱形,
当OP是菱形的对角线时,则PQ=OQ,
∵∠OPQ=45°,
∴∠OPQ=∠QOP=45°,
∴∠PQO=90°,
故可得点Q在OB中点处,
如图所示:

此时点M的坐标为(
| 2 |
当OP是菱形的一边时,
①若OQ=OP,如图所示:

此时点M的坐标为(
| 2 |
| 2 |
②若OM=OP,
如图所示:

此时△BQP≌△APO,则BP=OA=
| 2 |
| 2 |
过点P作PE⊥x轴于点E,
在等腰直角△APE中,PE=
| AP | ||
|
| 2 |
| 2 |
∵四边形MOPQ为菱形,
∴点M与点P关于y轴对称,
∴点M的坐标为(-1,
| 2 |
综上可得点M的坐标为:(
| ||
| 2 |
| 2 |
| 2 |
| 2 |
(3)如图所示:

点P运动 的3个界点位置分别是x=0,1,
| 3 |
| 2 |
当点P在点A处时,x1=0时,y1=
| 2 |
当点P在P1处时,x2=1时,y2=
| ||
| 2 |
故BQ2=y1-y2=
| 2 |
| ||
| 2 |
| ||
| 2 |
当点P位于点P3时,x3=
| 3 |
| 2 |
5
| ||
| 8 |
故Q2Q3=y3-y2=
| ||
| 8 |
点Q运动的路径长=BQ2+Q2Q3=
| ||
| 2 |
| ||
| 8 |
5
| ||
| 8 |
点评:本题考查了一次函数的综合题,涉及了菱形的判定与性质及等腰直角三角形的知识,用到了分类讨论的思想,分类讨论思想在数学解题中很重要,同学们注意认真掌握.

练习册系列答案
相关题目
下列事件是必然事件的是( )
| A、打开电视,正在播放足球比赛 |
| B、一个正数加上一个负数的和不是正数就是负数 |
| C、四边形四个内角的和是180° |
| D、三角形任意两边差小于第三边 |
 如图,在4×4正方形网格中,以格点为顶点的△ABC的面积等于3,则点A到边BC的距离为( )
如图,在4×4正方形网格中,以格点为顶点的△ABC的面积等于3,则点A到边BC的距离为( )A、
| ||
B、2
| ||
| C、4 | ||
| D、3 |
 如图,由转盘和箭头组成的A、B两个装置,其转盘分别被分成四个面积相等的扇形.装置A上的数字分别是1、2、7、8,装置B的数字分别是3、4、5、6.这两个装置除了表面数字不同外,其他构造完全相同.
如图,由转盘和箭头组成的A、B两个装置,其转盘分别被分成四个面积相等的扇形.装置A上的数字分别是1、2、7、8,装置B的数字分别是3、4、5、6.这两个装置除了表面数字不同外,其他构造完全相同. 如图,直线y=kx+1与反比例函数
如图,直线y=kx+1与反比例函数 如图,直线y=2x+b与双曲线y=
如图,直线y=2x+b与双曲线y=