题目内容
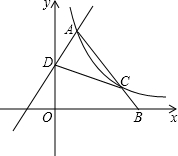 如图,直线y=2x+b与双曲线y=
如图,直线y=2x+b与双曲线y=| k |
| x |
考点:反比例函数与一次函数的交点问题
专题:
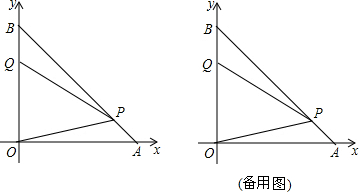
分析:过A作AQ⊥y轴于Q,AM⊥x轴于M,过C作CN⊥x轴于N,设A(x,y),则C(
,
y),把A、C的坐标代入反比例函数的解析式求出A的横坐标,再根据三角形面积求出即可.
| 6-x |
| 2 |
| 1 |
| 2 |
解答:
解:过A作AQ⊥y轴于Q,AM⊥x轴于M,过C作CN⊥x轴于N,
则AM∥CN,
∵AC=BC,
∴BN=NM,
∴bn=mn,CN=
AM,
∵B(6,0),
设A(x,y),则C(
,
y),
∵A、C都在反比例函数y=
上,
∴xy=
y,
解得:x=2,
即A(2,4+b),
∵△ACD的面积是8,
∴△BDC的面积是8(等底等高的三角形面积相等),
∴S四边形AQOB-S△ADQ-S△BOD=2×8,
∴
•(2+b)•(4+b)-
×2(4+b-b)-
•b•6=16,
解得:b=4,
即A的坐标是(2,8),
∴k=2×8=16,
故答案为:16.

解:过A作AQ⊥y轴于Q,AM⊥x轴于M,过C作CN⊥x轴于N,
则AM∥CN,
∵AC=BC,
∴BN=NM,
∴bn=mn,CN=
| 1 |
| 2 |
∵B(6,0),
设A(x,y),则C(
| 6-x |
| 2 |
| 1 |
| 2 |
∵A、C都在反比例函数y=
| k |
| x |
∴xy=
| 6-x |
| 2 |
解得:x=2,
即A(2,4+b),
∵△ACD的面积是8,
∴△BDC的面积是8(等底等高的三角形面积相等),
∴S四边形AQOB-S△ADQ-S△BOD=2×8,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解得:b=4,
即A的坐标是(2,8),
∴k=2×8=16,
故答案为:16.
点评:本题考查了用待定系数法求出反比例函数的解析式,三角形的面积等知识点的应用,主要考查学生的计算能力,题目综合性比较强,有一定的难度.

练习册系列答案
相关题目
如果手头没有硬币,下列方法可以模拟掷硬币实验的是( )

| A、掷一个瓶盖,盖面朝上代表正面,盖面朝下代表反面 |
| B、掷一枚图钉,钉尖着地代表正面,钉帽着地代表反面 |
| C、用计算器产生1和2两个随机整数,1代表正面,2代表反面 |
| D、转动如图所示的装盘,指针指向“红”代表正面,指针指向“蓝”代表反面 |
 如图,在10×10的正方形网格中,每个小正方形的边长均为单位1,在方格中作图:
如图,在10×10的正方形网格中,每个小正方形的边长均为单位1,在方格中作图: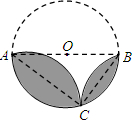 如图,AB是⊙O的直径,点C在⊙O上,将弦AC、BC所对的劣弧分别沿AC、BC翻折,将AB上方所对的半圆沿AB翻折.若AC=4,BC=3,则翻折后的三条弧组成两个“叶片形”图形(阴影部分)的周长和为
如图,AB是⊙O的直径,点C在⊙O上,将弦AC、BC所对的劣弧分别沿AC、BC翻折,将AB上方所对的半圆沿AB翻折.若AC=4,BC=3,则翻折后的三条弧组成两个“叶片形”图形(阴影部分)的周长和为