题目内容
3.关于x的一元二次方程mx2+2x-1=0有两个实数根,则m的取值范围是( )| A. | m≤-1 | B. | m≥-1 | C. | m≤1且m≠0 | D. | m≥-1且m≠0 |
分析 根据一元二次方程的定义以及根的判别式的意义可得△=4+4m≥0且m≠0,求出m的取值范围即可.
解答 解:∵关于x的一元二次方程mx2+2x-1=0有两个实数根,
∴△≥0且m≠0,
∴4+4m≥0且m≠0,
∴m≥-1且m≠0,
故选D.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)根的判别式△=b2-4ac.当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.也考查了一元二次方程的定义.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
13.下列图形可由平移得到的是( )
| A. |  | B. |  | C. |  | D. |  |
14.三角形的三边长分别为3,4,5,则最长边上的高为( )
| A. | $\frac{4}{3}$ | B. | 3 | C. | 4 | D. | $\frac{12}{5}$ |
8.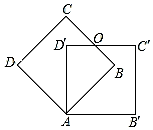 一顶点重合的两个大小完全相同的边长为3的正方形ABCD和正方形AB′C′D′,如图所示,∠DAD′=45°,边BC与D′C′交于点O,则四边形ABOD′的周长是( )
一顶点重合的两个大小完全相同的边长为3的正方形ABCD和正方形AB′C′D′,如图所示,∠DAD′=45°,边BC与D′C′交于点O,则四边形ABOD′的周长是( )
 一顶点重合的两个大小完全相同的边长为3的正方形ABCD和正方形AB′C′D′,如图所示,∠DAD′=45°,边BC与D′C′交于点O,则四边形ABOD′的周长是( )
一顶点重合的两个大小完全相同的边长为3的正方形ABCD和正方形AB′C′D′,如图所示,∠DAD′=45°,边BC与D′C′交于点O,则四边形ABOD′的周长是( )| A. | 6 | B. | 6$\sqrt{2}$ | C. | 3$\sqrt{2}$ | D. | 3+3$\sqrt{2}$ |
15.若x-$\frac{1}{x}$=3,则$\frac{{x}^{2}}{{x}^{4}+1}$=( )
| A. | 11 | B. | 7 | C. | $\frac{1}{11}$ | D. | $\frac{1}{7}$ |
12.菱形的边长是5,一条对角线长是6,则菱形的面积是( )
| A. | 48 | B. | 25 | C. | 24 | D. | 12 |
 如图所示是长方体的平面展开图,设AB=x,若AD=4x,AN=3x.
如图所示是长方体的平面展开图,设AB=x,若AD=4x,AN=3x. 如图,利用函数图象解方程组$\left\{\begin{array}{l}{x+2y=4}\\{2x-y=3}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$.
如图,利用函数图象解方程组$\left\{\begin{array}{l}{x+2y=4}\\{2x-y=3}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$.