题目内容
4．在实数范围内定义一种运算“*”，其规则为a*b=a（a-b），根据这个规则，方程（x+2）*5=0的解为x1=-2，x2=3．分析 根据新定义得到（x+2）（x+2-5）=0，然后利用因式分解法解方程．
解答 解：（x+2）（x+2-5）=0，
x+2=0或x+2-5=0，
所以x1=-2，x2=3．
故答案为x1=-2，x2=3．
点评 本题考查了解一元二次方程-因式分解法：先把方程的右边化为0，再把左边通过因式分解化为两个一次因式的积的形式，那么这两个因式的值就都有可能为0，这就能得到两个一元一次方程的解，这样也就把原方程进行了降次，把解一元二次方程转化为解一元一次方程的问题了（数学转化思想）．
练习册系列答案
相关题目
15．方程组$\left\{\begin{array}{l}{x+y=3}\\{x-y=1}\end{array}\right.$的解为（ ）
| A． | $\left\{\begin{array}{l}{x=3}\\{y=0}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x=3}\\{y=2}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$ |
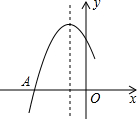如图是二次函数y=ax2+bx+c图象的一部分，图象过点A（-3，0），对称轴为x=-1．与x轴的另一个交点B．给出以下几个结论：①2a-b=0；②b＜0；③c＞0；④b2＞4ac ⑤点B的坐标是（1，0）．其中正确结论的序号是①②③④⑤．
已知二次函数y=x2-4x．
如图，AB=4，BC=3，AD=13，DC=12，∠B=90°，求四边形ABCD的面积．