题目内容
13.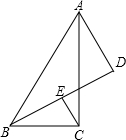 如图,在Rt△ABC中,∠ACB=90°,D为△ABC外一点,使∠DAC=∠BAC,E为BD的中点,∠ABC=60°,求∠ACE的度数.
如图,在Rt△ABC中,∠ACB=90°,D为△ABC外一点,使∠DAC=∠BAC,E为BD的中点,∠ABC=60°,求∠ACE的度数.
分析 延长AD、BC交于F,通过证△ABC≌△ACF即可得出∠ACE=∠CAF=30°.
解答  解:延长AD、BC交于F.
解:延长AD、BC交于F.
∵在△ABC与△ACF中,
$\left\{\begin{array}{l}{∠DAC=∠BAC}\\{AC=AC}\\{∠ACB=∠ACF=90°}\end{array}\right.$,
∴△ABC≌△ACF(ASA),
∴BC=FC,∠F=∠ABC=60°,
∴∠CAF=30°,
∵E为BD的中点,
∴EC∥AF,
∴∠ACE=∠CAF=30°.
点评 此题主要考查等腰三角形的判定及三角形中位线定理的综合运用.三角形的中位线平行于第三边且等于第三边的一半.

练习册系列答案
相关题目
3.函数y=$\frac{3}{x}$与y=x-1图象的一个交点的横、纵坐标分别为a、b,则$\frac{1}{a}$-$\frac{1}{b}$的值为( )
| A. | -$\frac{1}{3}$ | B. | $\frac{1}{3}$ | C. | 3 | D. | 1-3 |
5.若a=$\frac{1}{b}$-$\frac{1}{c}$,则c=( )
| A. | $\frac{1+ab}{b}$ | B. | b-$\frac{1}{a}$ | C. | b+$\frac{1}{a}$ | D. | $\frac{b}{1-ab}$ |
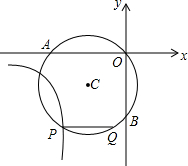 如图,过原点O的⊙C与两坐标轴分别交于点A(-4,0)、B(0,-3),在第三象限的⊙C上有一点P,过点P作弦PQ∥x轴,且PQ=3,已知双曲线y=$\frac{k}{x}$过点P,则k的值是$\frac{49}{4}$.
如图,过原点O的⊙C与两坐标轴分别交于点A(-4,0)、B(0,-3),在第三象限的⊙C上有一点P,过点P作弦PQ∥x轴,且PQ=3,已知双曲线y=$\frac{k}{x}$过点P,则k的值是$\frac{49}{4}$.