题目内容
点P为⊙O内一点,且OP=4,若⊙O的半径为6,则过点P的弦长不可能为
- A.12
- B.

- C.8
- D.10.5
C
分析:过点P最长的弦是圆的半径,最短的弦是与OP垂直的弦,所以过点P的弦最长是12,最短是 .
.
解答: 解:如图所示,OP⊥AB,
解:如图所示,OP⊥AB,
则AB是过点P最短的弦,
∴AP=BP,
OA=6,OP=4,
在Rt△AOP中,AP= ,
,
所以AB= .
.
由于8< ,所以过点P的弦长不可能为8.
,所以过点P的弦长不可能为8.
故选C.
点评:解决与弦有关的问题时,往往需构造以半径、弦心距和弦长的一半为三边的直角三角形,若设圆的半径为r,弦长为a,这条弦的弦心距为d,则有等式r2=d2+( )2成立,知道这三个量中的任意两个,就可以求出另外一个.
)2成立,知道这三个量中的任意两个,就可以求出另外一个.
分析:过点P最长的弦是圆的半径,最短的弦是与OP垂直的弦,所以过点P的弦最长是12,最短是
 .
.解答:
 解:如图所示,OP⊥AB,
解:如图所示,OP⊥AB,则AB是过点P最短的弦,
∴AP=BP,
OA=6,OP=4,
在Rt△AOP中,AP=
 ,
,所以AB=
 .
.由于8<
 ,所以过点P的弦长不可能为8.
,所以过点P的弦长不可能为8.故选C.
点评:解决与弦有关的问题时,往往需构造以半径、弦心距和弦长的一半为三边的直角三角形,若设圆的半径为r,弦长为a,这条弦的弦心距为d,则有等式r2=d2+(
 )2成立,知道这三个量中的任意两个,就可以求出另外一个.
)2成立,知道这三个量中的任意两个,就可以求出另外一个. 
练习册系列答案
相关题目
点P为⊙O内一点,且OP=4,若⊙O的半径为6,则过点P的弦长不可能为( )
| A、12 | ||
B、2
| ||
| C、8 | ||
| D、10.5 |
 如图,点P为⊙O内一点,且OP=6,若⊙O的半径为10,则过点P的弦长不可能为( )
如图,点P为⊙O内一点,且OP=6,若⊙O的半径为10,则过点P的弦长不可能为( )| A、20 | B、17.5 | C、16 | D、12 |
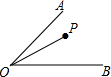 如图,∠AOB=45°,点P为∠AOB内一点,且OP=4,M为OA上一点,N为OB上一点,则△PMN的周长的最小值为( )
如图,∠AOB=45°,点P为∠AOB内一点,且OP=4,M为OA上一点,N为OB上一点,则△PMN的周长的最小值为( )A、4
| ||
B、4
| ||
| C、4 | ||
D、2
|
 如图,已知:点M为⊙O内一点,且过点M最长的弦为10cm,最短的弦为6cm,则OM的长为
如图,已知:点M为⊙O内一点,且过点M最长的弦为10cm,最短的弦为6cm,则OM的长为 如图,⊙O半径是
如图,⊙O半径是