Question

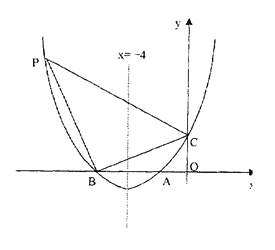
【题目】如图,已知抛物线的对称轴是x=－4,抛物线与x轴交于A,B两点,与y轴交于C点,O是坐标原点,且A,C的坐标分别是(－2,0),(0,3).

（1）求抛物线的解析式；

（2）抛物线上有一点是P,满足∠PBC=90,求P点的坐标；

（3）y轴上是否存在点E使得△AOE与△PBC相似?若存在求出点E的坐标,若不存在,请说明理由.

Answer 1

【答案】（1）y=x2+2x+3 ；（2）（-10，8）；（3）（0，）和（0，-）.

【解析】

根据对称性写出B点坐标，再设参数解方程求得抛物线解析式；利用相似三角形的判定及性质定理及抛物线解析式解出P坐标；第三问同样借助相似三角形性质定理解答.

（1）抛物线的对称轴是x=－4，A的坐标是(－2,0)，则B坐标为(-6,0)，设,把AB两点坐标带入得：,解得,抛物线解析式为 y=x2+2x+3；（2）过P作PF,所以,从而,又OB=6,OC=3,故PF=2BF,设BF=m则PF=2m，OF=6+m,P坐标为（-6-m,2m）,由点P在抛物线上可得2m=,解得m1=0(舍去),m2=4，故P（-10，8）；（3）设E坐标为（0，n）,由已知得BC=,PB=4,若△AOE△PBC，则,,n=,所以存在E点，E点坐标为（0，）和（0，-）.