题目内容
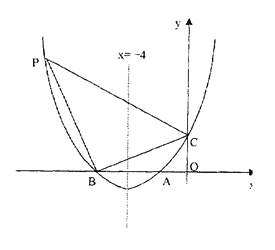
【题目】已知二次函数
，点
在该函数的图象上，点到
轴、
轴的距离分别为
、
．设
，下列结论中：
①
没有最大值；②没有最小值；③
时，随的增大而增大；
④满足
的点有四个．其中正确结论的个数有（ ）
A. 
个 B. 
个 C. 
个 D. 
个
【答案】B
【解析】
找出二次函数与
轴的交点，结合点
所在的象限分段考虑，再根据二次函数的性质找出其最值以及在各段区间内的增减性，对比4个结论即可得知正确的结论有两个.
令二次函数
中
，即
，
解得：
，
.
（1）当
时，
，
，
，
；
（2）当
时，
，，
，
；
（3）当
时，，
，
，
（4）当
时，，，
，
.
综合可知：
有最小值，没有最大值，即①成立，②不成立；
当
时，随的增大而增大，
时，随的增大而减小，
时，随的增大而增大，结论③不成立；
令
，（1）中存在一个解；（2）中无解；（3）中有两个解；（4）中一个解.
满足的点有四个，结论④成立，
正确的结论有
个.
故选：
.
练习册系列答案
相关题目
【题目】某商场一品牌服装，销售一件可获利
元，为在十一期间增加盈利，进行促销活动，决定采取降价措施．根据以往销售经验及市场调查发现，每件服装降价
（元）与每天的销售量
（件）之间的关系如下表
|
|
|
|
|
| … |
|
|
|
|
|
| … |
请你按照上表，求与之间的函数解析式．
为保证每天能盈利
元，又能吸引顾客，每件服装应降价多少元？
