题目内容
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段CD上一点,且∠AFE=∠B。
(1)求证△ADF∽△DEC;
(2)若AB=4,AD=3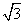 ,AE=3,求AF的长.
,AE=3,求AF的长.
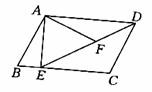
(1)∵四边形ABCD 是平行四边形∴∠ADF=∠CED,∠C+∠B=180°。
又∠AFD+∠AFE=180°,∠AFE=∠B,
∴∠AFD=∠C,∴△ADF∽△DEC。
(2)∵AB=4,AD=3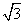 ,AE=3, AE⊥BC,∴AE⊥AD,CD=AB=4。
,AE=3, AE⊥BC,∴AE⊥AD,CD=AB=4。
在Rt△ADE中,由勾股定理得:DE=6
 由△ADF∽△DEC,得
由△ADF∽△DEC,得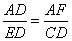 ,即
,即 ,解得:AF=2
,解得:AF=2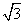

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
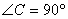 ,AB的垂直平分线交AC于点D,连接BD.若AC=2,
,AB的垂直平分线交AC于点D,连接BD.若AC=2,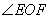 的度数;
的度数; ,则
,则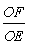 的值为 .
的值为 . 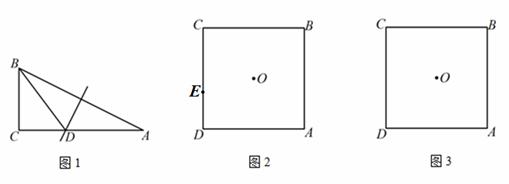
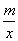 的图象的一个交点的坐标为(-1,-2),则另一个交点的坐标是 .
的图象的一个交点的坐标为(-1,-2),则另一个交点的坐标是 .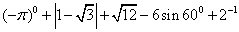
 (3)在(2)的条件下,设CQ=x,两块三角板重叠面积为y,求y与x的函数关系式.(图(2),图(3)供解题用)
(3)在(2)的条件下,设CQ=x,两块三角板重叠面积为y,求y与x的函数关系式.(图(2),图(3)供解题用)