Question

【题目】已知二次函数y=ax2(a≠0)与一次函数y=kx-2的图象相交于A.B两点,如图所示,其中A(-1,-1).

(1)求二次函数和一次函数的解析式;

(2)求△OAB的面积.

Answer 1

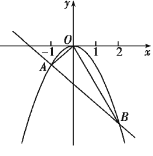
【答案】（1）y=-x2；（2）3

【解析】

（1）利用点A的坐标可求出直线与抛物线的解析式；

（2）求出点G的坐标及点B的坐标，利用S△OAB=OG|A的横坐标|+OG点B的横坐标求解即可．

(1)∵一次函数y=kx-2的图象过点A(-1,-1),

∴-1=-k-2,解得k=-1,

∴一次函数的解析式为y=-x-2.

∵y=ax2过点A(-1,-1),

∴-1=a×(-1)2,解得a=-1,

∴二次函数的解析式为y=-x2.

(2)设AB交y轴于点G,过B作BH⊥OG于点H.

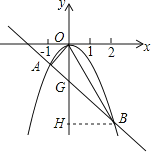
在y=-x-2中,令x=0,得y=-2,

∴G(0,-2),

联立一次函数与二次函数解析式可得

解得或

∴B(2,-4),∴BH=2.

∴S△OAB=S△AOG+S△BOG=×2×1+×2×2=1+2=3.