题目内容
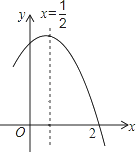
如图是二次函数y=ax2+bx+c（a≠0）图象的一部分，对称轴为x=
，且经过点（2，0），有下列说法：
①abc＜0；②a+b=0；③4a+2b+c＜0；④若（0，y1），（1，y2）是抛物线上的两点，则y1=y2．上述说法正确的是（ ）
|
| A． | ①②④ | B． | ③④ | C． | ①③④ | D． | ①② |
A解：①∵二次函数的图象开口向下，
∴a＜0，
∵二次函数的图象交y轴的正半轴于一点，
∴c＞0，
∵对称轴是直线x=，
∴﹣
，
∴b=﹣a＞0，
∴abc＜0．
故①正确；
②∵由①中知b=﹣a，
∴a+b=0，
故②正确；
③把x=2代入y=ax2+bx+c得：y=4a+2b+c，
∵抛物线经过点（2，0），
∴当x=2时，y=0，即4a+2b+c=0．
故③错误；
④∵（0，y1）关于直线x=
的对称点的坐标是（1，y1），
∴y1=y2．
故④正确；
综上所述，正确的结论是①②④．
练习册系列答案
考前必练系列答案
相关题目
÷（
﹣1），其中x=2﹣
．定义[x]为不超过x的最大整数，如[3.6]=3，[0.6]=0，[﹣3.6]=﹣4．对于任意实数x，下列式子中错误的是（ ）
|
| A． | [x]=x（x为整数） | B． | 0≤x﹣[x]＜1 |
|
| C． | [x+y]≤[x]+[y] | D． | [n+x]=n+[x]（n为整数） |
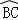上任意一点，过点P分别作AB，CD的垂线，垂足分别为N，M．
，BE=6，求OE的长．
×（﹣
）+|﹣2
|+（
）﹣3．
