题目内容
如图,在△ABC中,∠ABC=90°,以AB的中点O为圆心、OA为半径的圆交AC于点D,E是BC的中点,连接DE,OE.
(1)判断DE与⊙O的位置关系,并说明理由;
(2)求证:BC2=CD•2OE;
(3)若cos∠BAD= ,BE=6,求OE的长.
,BE=6,求OE的长.

(1)证明:连接OD,BD,
∵AB为圆O的直径,
∴∠ADB=90°,
在Rt△BDC中,E为斜边BC的中点,
∴CE=DE=BE= BC,
BC,
∴∠C=∠CDE,
∵OA=OD,
∴∠A=∠ADO,
∵∠ABC=90°,即∠C+∠A=90°,
∴∠AD O+∠CDE=90°,即∠ODE=90°,
O+∠CDE=90°,即∠ODE=90°,
∴DE⊥OD,又OD为圆的半径,
∴DE为⊙O的切线;
(2)证明:∵E是BC的中点,O点是AB的中点,
∴OE是△ABC的中位线,
∴AC=2OE,
∵∠C=∠C,∠ABC=∠BDC,
∴△ABC∽△BDC,
∴ =
= ,即BC2=AC•CD.
,即BC2=AC•CD.
∴BC2=2CD•OE;
(3)解:∵cos∠BAD= ,
,
∴sin∠BAC= =
= ,
,
又∵BE=6,E是BC的中点,即BC=12,
∴AC=15.
又∵AC=2OE,
∴OE= AC=
AC= .
.


如图是一个可以自由转动的转盘,转盘分为6个大小相同的扇形,指针的位置固定,转动的转盘停止后,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,当作指向右边的扇形),指针指向阴影区域的概率是( )

|
| A. |
| B. |
| C. |
| D. |
|
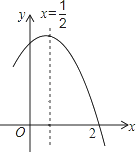
如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为x= ,且经过点(2,0),有下列说法:
,且经过点(2,0),有下列说法: ①abc<0;②a+b=0;③4a+2b+c<0;④若(0,y1),(1,y2)是抛物线上的两点,则y1=y2.上述说法正确的是( )
①abc<0;②a+b=0;③4a+2b+c<0;④若(0,y1),(1,y2)是抛物线上的两点,则y1=y2.上述说法正确的是( )
|
| A. | ①②④ | B. | ③④ | C. | ①③④ | D. | ①② |
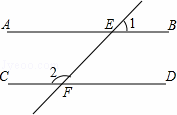
如图,AB∥CD,直线EF分别交直线AB,CD于点E,F.若∠1=46°30′,则∠1的度数为( )
|
| A. | 43°30′ | B. | 53°30′ | C. | 133°30′ | D. | 153°30′ |




 +2﹣x)÷
+2﹣x)÷ ,其中x满足x2﹣4x+3=0.
,其中x满足x2﹣4x+3=0. ,π,0,﹣6由小到大用“<”号连起来,可表示为
,π,0,﹣6由小到大用“<”号连起来,可表示为  统计图,则参加人数最多的课外兴趣小组是 ( )
统计图,则参加人数最多的课外兴趣小组是 ( )
