Question

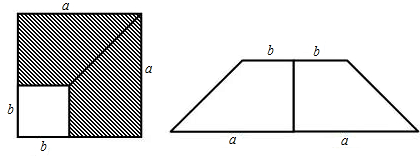
分别计算图（1）、（2）、（3）中阴影部分的面积，你发现了什么规律？

Answer 1

分析：根据已知图形得出各圆的半径，进而利用圆的面积公式得出阴影部分面积即可．

解答：解：由题意得：图形（1）中圆的半径为：

a

2

，
则图形（1）的阴影部分面积为：a²-π×（

a

2

）²=a²-

πa2

4

，
由题意得：图形（2）中圆的半径为：

a

4

，
则图形（2）的阴影部分面积为：a²-4×π×（

a

4

）²=a²-

πa2

4

，
由题意得：图形（3）中圆的半径为：

a

6

，
则图形（3）的阴影部分面积为：a²-9×π×（

a

6

）²=a²-

πa2

4

，
故图（1）、（2）、（3）中阴影部分的面积相等．

点评：此题主要考查了正方形的性质以及圆的面积公式，根据已知得出各图形中圆的半径是解题关键．