题目内容
19.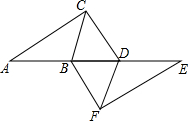 如图,点A、B、D、E在同一直线上,AD=EB,BC∥DF,∠A=∠E,连接CD,BF,试探索CD与FB的关系.
如图,点A、B、D、E在同一直线上,AD=EB,BC∥DF,∠A=∠E,连接CD,BF,试探索CD与FB的关系.
分析 CD=FB,CD∥FB.先根据ASA证明△ABC≌△EDF,再根据SAS证明△ACD≌△EFB,即可得出结论.
解答 解:CD=FB,CD∥FB.
理由:∵BC∥DF,
∴∠CBD=∠FDB,
∴∠ABC=∠EDF,
∵AD=EB,
∴AB=ED,
在△ABC和△EDF中,
$\left\{\begin{array}{l}{∠A=∠E}\\{AB=ED}\\{∠ABC=∠EDF}\end{array}\right.$,
∴△ABC≌△EDF,
∴AC=EF,
在△ACD和△EFB中,
$\left\{\begin{array}{l}{AC=EF}\\{∠A=∠E}\\{AD=EB}\end{array}\right.$,
∴△ACD≌△EFB,
∴CD=BF,∠ADC=∠EBF,
∴CD∥FB.
点评 本题考查了全等三角形的判定与性质及平行线的性质,三角形全等问题一般以考查三角形全等的方法为主,判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,寻找条件.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
9.下列调查适合用普查方式的是( )
| A. | 调查一沓钞票中有没有假钞 | B. | 调查我市中学生课外阅读的时间 | ||
| C. | 调查本市居民的年人均消费 | D. | 调查某种灯泡的使用寿命 |
11.若-3+( )=0,则( )中的数应该是( )
| A. | 3 | B. | -3 | C. | $-\frac{1}{3}$ | D. | $\frac{1}{3}$ |
9.-32的相反数是( )
| A. | 6 | B. | -6 | C. | 9 | D. | -9 |
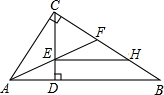 在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AE平分∠CAB交CD于点F,交CB于点E,过点E作EH∥AB,交BC于H.
在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AE平分∠CAB交CD于点F,交CB于点E,过点E作EH∥AB,交BC于H.
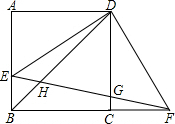 如图,正方形ABCD的边长为1,点E在边AB上,连接ED,过点D作FD⊥DE与BC的延长线交于点F,连接EF与CD交于点G、与对角线BD相交于点H
如图,正方形ABCD的边长为1,点E在边AB上,连接ED,过点D作FD⊥DE与BC的延长线交于点F,连接EF与CD交于点G、与对角线BD相交于点H