题目内容
【题目】阅读理解:在平面直角坐标系中,任意两点![]() ,
,![]() 之间的位置关系有以下三种情形;
之间的位置关系有以下三种情形;
①如果![]() 轴,则
轴,则![]() ,
,![]()
②如果![]() 轴,则
轴,则![]() ,
,![]()
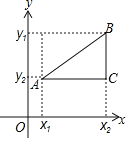
③如果![]() 与
与![]() 轴、
轴、![]() 轴均不平行,如图,过点
轴均不平行,如图,过点![]() 作与
作与![]() 轴的平行线与过点
轴的平行线与过点![]() 作与
作与![]() 轴的平行线相交于点
轴的平行线相交于点![]() ,则点
,则点![]() 坐标为
坐标为![]() ,由①得
,由①得![]() ;由②得
;由②得![]() ;根据勾股定理可得平面直角坐标系中任意两点的距离公式
;根据勾股定理可得平面直角坐标系中任意两点的距离公式![]() .
.
(1)若点![]() 坐标为
坐标为![]() ,点
,点![]() 坐标为
坐标为![]() 则
则![]() ________;
________;
(2)若点![]() 坐标为
坐标为![]() ,点
,点![]() 坐标为
坐标为![]() ,点
,点![]() 是
是![]() 轴上的动点,直接写出
轴上的动点,直接写出![]() 最小值=_______;
最小值=_______;
(3)已知![]() ,
,![]() 根据数形结合,求出
根据数形结合,求出![]() 的最小值?
的最小值?![]() 的最大值?
的最大值?
【答案】(1)5;(2)3![]() ;(3)M最小值=
;(3)M最小值=![]() ,N最大值=
,N最大值=![]() .
.
【解析】
(1)利用两点间的距离公式AB=![]() 计算;
计算;
(2)利用轴对称的性质求得点P的坐标以及AP+PB的最小值;
(3)利用M、N所表示的几何意义解答.
解:(1)AB=![]() =5;
=5;
故答案是:5;
(2)如图,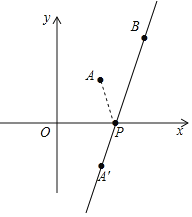
∵点A坐标为(3,3),
∴点A关于x轴对称的点A′的坐标是(3,-3),
此时AP+PB=A′B=![]() ,
,
故答案是:3![]() ;
;
(3)M=![]() ,
,
当M取最小值时,M表示点(x,0)与点(6,4)的距离与点(x,0)与点 (3,2)的距离之和(或M表示点(x,0)与点(6,-4)的距离与点(x,0)与点 (3,-2)的距离之和),
此时M最小值=![]() ,
,
N=![]() ,当N取最大值时,N表示点(x,0)与点(6,-4)的距离与点(x,0)与点 (3,2)的距离之差(或M表示点(x,0)与点(6,-4)的距离与点(x,0)与点 (3,2)的距离之差),
,当N取最大值时,N表示点(x,0)与点(6,-4)的距离与点(x,0)与点 (3,2)的距离之差(或M表示点(x,0)与点(6,-4)的距离与点(x,0)与点 (3,2)的距离之差),
此时N最大值=![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】为加强公民节电意识,某县将居民用电量分为两个阶梯,月用电量不超过![]() 度时按第一个阶梯费用收费,超过
度时按第一个阶梯费用收费,超过![]() 度时,超出的部分按第二个阶梯费用收费下表是该县居民肖伟家2019年3月和4月所交电费的收据.求该县居民用电第--阶梯电费和第二阶梯电费分别为每度多少元?
度时,超出的部分按第二个阶梯费用收费下表是该县居民肖伟家2019年3月和4月所交电费的收据.求该县居民用电第--阶梯电费和第二阶梯电费分别为每度多少元?
电费收据(幸福里小区电费专用章)
户名 | 肖伟 |
电表号 |
|
月份 | 3月 |
用电量 |
|
金额 |
|
2019年3月收费员林云
电费收据(幸福里小区电费专用章)
户名 | 肖伟 |
电表号 |
|
月份 | 4月 |
用电量 |
|
金额 |
|
2019年4月收费员林云