Question

【题目】如图，在Rt△ABC中，AC=BC，∠ACB=90°，点D，E分别在AC，BC上，且CD=CE．

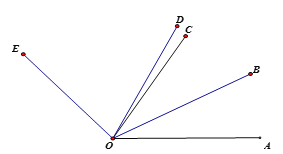
（1）如图1，求证：∠CAE=∠CBD；

（2）如图2，F是BD的中点，求证：AE⊥CF；

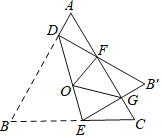
（3）如图3，F，G分别是BD，AE的中点，若AC=2，CE=1，求△CGF的面积．

Answer 1

【答案】（1）证明见解析；（2）证明见解析；（3）S△CFG=．

【解析】

（1）直接判断出△ACE≌△BCD即可得出结论；

（2）先判断出∠BCF=∠CBF，进而得出∠BCF=∠CAE，即可得出结论；

（3）先求出BD=3，进而求出CF=，同理：EG=，再利用等面积法求出ME，进而求出GM，最后用面积公式即可得出结论．

（1）在△ACE和△BCD中，

，

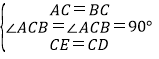∴△ACE≌△BCD，

∴∠CAE=∠CBD；

（2）如图2，

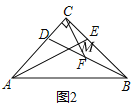
在Rt△BCD中，点F是BD的中点，

∴CF=BF，

∴∠BCF=∠CBF，

由（1）知，∠CAE=∠CBD，

∴∠BCF=∠CAE，

∴∠CAE+∠ACF=∠BCF+∠ACF=∠BAC=90°，

∴∠AMC=90°，

∴AE⊥CF；

（3）如图3，

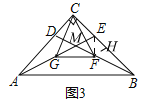
∵AC=2，

∴BC=AC=2，

∵CE=1，

∴CD=CE=1，

在Rt△BCD中，根据勾股定理得，BD==3，

∵点F是BD中点，

∴CF=DF=BD=，

同理：EG=AE=，

连接EF，过点F作FH⊥BC，

∵∠ACB=90°，点F是BD的中点，

∴FH=CD=，

∴S△CEF=CEFH=×1×=，

由（2）知，AE⊥CF，

∴S△CEF=CFME=×ME=ME，

∴ME=，

∴ME=，

∴GM=EG-ME=-=，

∴S△CFG=CFGM=××=．