题目内容
2.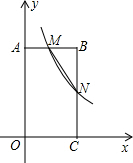 如图,在直角坐标系中,矩形OABC的顶点0与坐标原点重合,A、C分别在坐标轴上,点B的坐标为(2,4),直线y=-2x+6交AB、BC分别于点M、N,反比例函数y=$\frac{k}{x}$的图象经过点M.
如图,在直角坐标系中,矩形OABC的顶点0与坐标原点重合,A、C分别在坐标轴上,点B的坐标为(2,4),直线y=-2x+6交AB、BC分别于点M、N,反比例函数y=$\frac{k}{x}$的图象经过点M.(1)求反比例函数的解析式,并验证N点在该反比例函数图象上;
(2)若点P在y轴上,且△OPM的面积与四边形BMON的面积相等,求点P的坐标.
分析 (1)将y=4代入y=-2x+6得出M(1,4),把M的坐标代入y=$\frac{k}{x}$即可求得反比例函数的解析式,把x=2代入直线的解析式即可求出N的坐标,然后代入反比例函数的解析式验证即可.
(2)先求得S四边形BMON=S矩形OABC-S△AOM-S△CON=4,根据题意得出$\frac{1}{2}$OP•AM=4,进而求得OP=8,即可求得P的坐标.
解答 解:(1)∵B(2,4)四边形OABC是矩形,
∴OA=BC=4,
将y=4代入y=-2x+6得,x=1,
∴M(1,4),
把M的坐标代入y=$\frac{k}{x}$得,k=4,
∴反比例函数的解析式是y=$\frac{4}{x}$,
把x=2代入y=-2x+6得,y=2,
∴N(2,2),
把x=2代入y=$\frac{4}{x}$得,y=2,
∴N点在该反比例函数图象上;
(2)∵S四边形BMON=S矩形OABC-S△AOM-S△CON=4×2-$\frac{1}{2}$×1×4-$\frac{1}{2}$×2×2=4,
由题意得,$\frac{1}{2}$OP•AM=4,
∵AM=1,
∴OP=8,
∴点P的坐标为(0,8)或(0,-8).
点评 本题考查了用待定系数法反比例函数的解析式,函数图象上点的坐标特征,三角形的面积,矩形的性质的应用,主要考查学生综合运用性质进行推理和计算的能力,有一定的难度.

练习册系列答案
 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
10.将抛物线y=x2向右平移3个单位得到的抛物线表达式是( )
| A. | y=(x-3)2 | B. | y=(x+3)2 | C. | y=x2-3 | D. | y=x2+3 |
11.某中学为筹备校庆活动,准备印制一批校庆纪念册,该纪念册每册需要10张8K大小的纸,其中4张为彩页,6张为黑白页.印制该纪念册的总费用由制版费和印刷费两部分组成,制版费与印数无关,价格为:彩页300元/张,黑白页50元/张,印刷费与印数的关系见下表:
(1)印制这批纪念册的制版费为1500元;
(2)若印制2千册,则共需多少费用?
| 印数a(单位:千册) | 1≤a<5 | 5≤a<10 |
| 彩色(单位:元/张) | 2.2 | 2.0 |
| 黑白(单位:元/张) | 0.8 | 0.6 |
(2)若印制2千册,则共需多少费用?
12.零售商小张获得了某公司为期60天的新产品销售权,已知该产品的成本为35元/件,经调查,此商品在第x天的销售量p件与销售天数x的关系如下表:
销售单位q(元/件)与x满足:当1≤x<45时,q=x+55;当45≤x≤60时,q=35+$\frac{2925}{x}$.
(1)请分析表格中销售量p与x的关系,请直接写出销售量p与x的关系;
(2)请求出这60天内小张获得的最大日销售利润;
(3)为调动零售商积极性,公司在销售开始的前45天内,每售出一件商品,公司返m(m≥10)元给零售商,通过调查发现,当x≤30时,小张获得返现后的日销售利润随x的增大而增大,求m的取值范围.
| x(天) | 1 | 2 | 3 | … | 60 |
| p(件) | 198 | 196 | 194 | 80 |
(1)请分析表格中销售量p与x的关系,请直接写出销售量p与x的关系;
(2)请求出这60天内小张获得的最大日销售利润;
(3)为调动零售商积极性,公司在销售开始的前45天内,每售出一件商品,公司返m(m≥10)元给零售商,通过调查发现,当x≤30时,小张获得返现后的日销售利润随x的增大而增大,求m的取值范围.
 如图,正方形ABCD的边长为6,点E在边AB上,连接ED,过点D作FD⊥DE与BC的延长线相交于点F,连接EF与边CD相交于点G、与对角线BD相交于点H.
如图,正方形ABCD的边长为6,点E在边AB上,连接ED,过点D作FD⊥DE与BC的延长线相交于点F,连接EF与边CD相交于点G、与对角线BD相交于点H.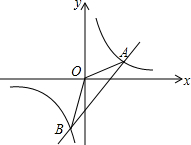 如图,已知一次函数y=kx-3的图象与反比例函数y=$\frac{m}{x}$(m为常数,且m≠0)的图象交于A、B两点,点A的坐标为(4,1);
如图,已知一次函数y=kx-3的图象与反比例函数y=$\frac{m}{x}$(m为常数,且m≠0)的图象交于A、B两点,点A的坐标为(4,1);