题目内容
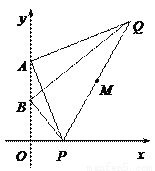
如图,A、B两点的坐标分别为(0,4),(0,2),点P为x轴正半轴上一动点,过点A作AP的垂线,过点B作BP的垂线,两垂线交于点Q,连接PQ,M为线段PQ的中点.
(1)求证:A、B、P、Q四点在以M为圆心的同一个圆上;
(2)当⊙M与x轴相切时,求点Q的坐标;
(3)当点P从点(1,0)运动到点(2,0)时,请直接写出线段QM扫过图形的面积.


练习册系列答案
相关题目
题目内容
如图,A、B两点的坐标分别为(0,4),(0,2),点P为x轴正半轴上一动点,过点A作AP的垂线,过点B作BP的垂线,两垂线交于点Q,连接PQ,M为线段PQ的中点.
(1)求证:A、B、P、Q四点在以M为圆心的同一个圆上;
(2)当⊙M与x轴相切时,求点Q的坐标;
(3)当点P从点(1,0)运动到点(2,0)时,请直接写出线段QM扫过图形的面积.


