题目内容
1.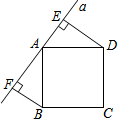 如图所示,直线a经过正方形ABCD的顶点A,分别过正方形的顶点B、D作BF⊥a于点F,DE⊥a于点E.若DE=7,BF=5,则EF的长为12.
如图所示,直线a经过正方形ABCD的顶点A,分别过正方形的顶点B、D作BF⊥a于点F,DE⊥a于点E.若DE=7,BF=5,则EF的长为12.
分析 首先证明∠ABF=∠EAD,再利用AAS定理证明△AED≌△BFA,进而得到AF=ED=7,AE=BF,然后再根据线段的和差关系可得答案.
解答 解:∵四边形ABCD是正方形,
∴∠BAD=90°,AD=AB,
∴∠DAE+∠BAF=90°,
∵BF⊥EF,
∴∠BAF+∠ABF=90°,
∴∠ABF=∠EAD,
在△ABF和△DAE中,$\left\{\begin{array}{l}{∠AED=∠AFB}\\{∠ABF=∠EAD}\\{AD=AB}\end{array}\right.$,
∴△AED≌△BFA(AAS),
∴AF=ED=7,AE=BF,
∴EF=AE+AF=BF+ED=7+5=12.
故答案为:12.
点评 本题考查了平行四边形性质,平行线性质,全等三角形的性质和判定的应用,关键是推出△AED≌△BFA.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
16.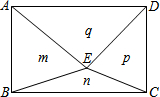 如图,E是矩形ABCD内的一个动点,连接EA、EB、EC、ED,得到△EAB、△EBC、△ECD、△EDA,设它们的面积分别是m、n、p、q,给出如下结论:
如图,E是矩形ABCD内的一个动点,连接EA、EB、EC、ED,得到△EAB、△EBC、△ECD、△EDA,设它们的面积分别是m、n、p、q,给出如下结论:
①m+n=q+p;
②m+p=n+q;
③若m=n,则E点一定是AC与BD的交点;
④若m=n,则E点一定在BD上.
其中正确结论的序号是( )
 如图,E是矩形ABCD内的一个动点,连接EA、EB、EC、ED,得到△EAB、△EBC、△ECD、△EDA,设它们的面积分别是m、n、p、q,给出如下结论:
如图,E是矩形ABCD内的一个动点,连接EA、EB、EC、ED,得到△EAB、△EBC、△ECD、△EDA,设它们的面积分别是m、n、p、q,给出如下结论:①m+n=q+p;
②m+p=n+q;
③若m=n,则E点一定是AC与BD的交点;
④若m=n,则E点一定在BD上.
其中正确结论的序号是( )
| A. | ①③ | B. | ②④ | C. | ①②③ | D. | ②③④ |
6.下列现象是数学中的平移的是( )
| A. | 骑自行车时的轮胎滚动 | |
| B. | 碟片在光驱中运行 | |
| C. | “神舟”十号宇宙飞船绕地球运动 | |
| D. | 生产中传送带上的电视机的移动过程 |
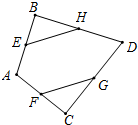 如图,在四边形ABCD中,AB=AC,DB⊥AB,DC⊥AC,且E,F,G,H分别为AB,AC,CD,BD的中点.
如图,在四边形ABCD中,AB=AC,DB⊥AB,DC⊥AC,且E,F,G,H分别为AB,AC,CD,BD的中点.