题目内容
已知关于x的方程x2+(1-m)x+
=0有两个不相等的实数根,则m的最大整数值是 .
| m2 |
| 4 |
考点:根的判别式
专题:判别式法
分析:根据判别式的意义得到△=(1-m)2-4×
>0,然后解不等式得到m的取值范围,再在此范围内找出最大整数即可.
| m2 |
| 4 |
解答:解:根据题意得△=(1-m)2-4×
>0,
解得m<
,
所以m的最大整数值为0.
故答案为:0.
| m2 |
| 4 |
解得m<
| 1 |
| 2 |
所以m的最大整数值为0.
故答案为:0.
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
已知等腰三角形的其中二边长分别为4,9,则这个等腰三角形的周长为( )
| A、17 | B、22 |
| C、17或22 | D、无法确定 |
 如图,方格纸中每个小正方形的边长均为1,四边形ABCD的四个顶点都在小正方形的顶点上,点E在BC边上,且点E在小正方形的顶点上,连接AE.
如图,方格纸中每个小正方形的边长均为1,四边形ABCD的四个顶点都在小正方形的顶点上,点E在BC边上,且点E在小正方形的顶点上,连接AE.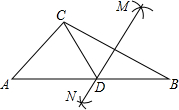 如图,在△ABC中,按以下步骤作图:
如图,在△ABC中,按以下步骤作图: 如图,直线a、b被直线c所截,a∥b,∠1+∠2的度数是
如图,直线a、b被直线c所截,a∥b,∠1+∠2的度数是