题目内容
 (2012•临沂)如图,点A、F、C、D在同一直线上,点B和点E分别在直线AD的两侧,且AB=DE,∠A=∠D,AF=DC.
(2012•临沂)如图,点A、F、C、D在同一直线上,点B和点E分别在直线AD的两侧,且AB=DE,∠A=∠D,AF=DC.(1)求证:四边形BCEF是平行四边形,
(2)若∠ABC=90°,AB=4,BC=3,当AF为何值时,四边形BCEF是菱形.
分析:(1)由AB=DE,∠A=∠D,AF=DC,易证得△ABC≌DEF,即可得BC=EF,且BC∥EF,即可判定四边形BCEF是平行四边形;
(2)由四边形BCEF是平行四边形,可得当BE⊥CF时,四边形BCEF是菱形,所以连接BE,交CF与点G,证得△ABC∽△BGC,由相似三角形的对应边成比例,即可求得AF的值.
(2)由四边形BCEF是平行四边形,可得当BE⊥CF时,四边形BCEF是菱形,所以连接BE,交CF与点G,证得△ABC∽△BGC,由相似三角形的对应边成比例,即可求得AF的值.
解答:(1)证明:∵AF=DC,
∴AF+FC=DC+FC,即AC=DF.
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS),
∴BC=EF,∠ACB=∠DFE,
∴BC∥EF,
∴四边形BCEF是平行四边形.
 (2)解:连接BE,交CF于点G,
(2)解:连接BE,交CF于点G,
∵四边形BCEF是平行四边形,
∴当BE⊥CF时,四边形BCEF是菱形,
∵∠ABC=90°,AB=4,BC=3,
∴AC=
=5,
∵∠BGC=∠ABC=90°,∠ACB=∠BCG,
∴△ABC∽△BGC,
∴
=
,
即
=
,
∴CG=
,
∵FG=CG,
∴FC=2CG=
,
∴AF=AC-FC=5-
=
,
∴当AF=
时,四边形BCEF是菱形.
∴AF+FC=DC+FC,即AC=DF.
在△ABC和△DEF中,
|
∴△ABC≌△DEF(SAS),
∴BC=EF,∠ACB=∠DFE,
∴BC∥EF,
∴四边形BCEF是平行四边形.
 (2)解:连接BE,交CF于点G,
(2)解:连接BE,交CF于点G,∵四边形BCEF是平行四边形,
∴当BE⊥CF时,四边形BCEF是菱形,
∵∠ABC=90°,AB=4,BC=3,
∴AC=
| AB2+BC2 |
∵∠BGC=∠ABC=90°,∠ACB=∠BCG,
∴△ABC∽△BGC,
∴
| BC |
| AC |
| CG |
| BC |
即
| 3 |
| 5 |
| CG |
| 3 |
∴CG=
| 9 |
| 5 |
∵FG=CG,
∴FC=2CG=
| 18 |
| 5 |
∴AF=AC-FC=5-
| 18 |
| 5 |
| 7 |
| 5 |
∴当AF=
| 7 |
| 5 |
点评:此题考查了相似三角形的判定与性质、全等三角形的判定与性质、平行四边形的判定与性质、菱形的判定与性质以及勾股定理等知识.此题综合性较强,难度适中,注意数形结合思想的应用,注意掌握辅助线的作法.

练习册系列答案
相关题目
 (2012•临沂)如图,AB∥CD,DB⊥BC,∠1=40°,则∠2的度数是( )
(2012•临沂)如图,AB∥CD,DB⊥BC,∠1=40°,则∠2的度数是( ) (2012•临沂)如图是一个几何体的三视图,则这个几何体的侧面积是( )
(2012•临沂)如图是一个几何体的三视图,则这个几何体的侧面积是( )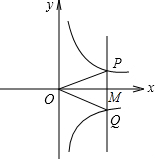 (2012•临沂)如图,若点M是x轴正半轴上任意一点,过点M作PQ∥y轴,分别交函数y=
(2012•临沂)如图,若点M是x轴正半轴上任意一点,过点M作PQ∥y轴,分别交函数y= (2012•临沂)如图,AB是⊙O的直径,点E为BC的中点,AB=4,∠BED=120°,则图中阴影部分的面积之和为( )
(2012•临沂)如图,AB是⊙O的直径,点E为BC的中点,AB=4,∠BED=120°,则图中阴影部分的面积之和为( )