题目内容
10．观察图形，它们是按一定规律排列的，依照此规律，第n个图形中★的个数是2n+2个．
分析 由图形可知：第1个图形中★的个数是4个，第2个图形中★的个数是4+2=6个，第3个图形中★的个数是4+2×2=8个，第4个图形中★的个数是4+2×3=10个，…由此得出第n个图形中★的个数是4+2（n-1）=2n+2个．
解答 解：∵第1个图形中★的个数是4个，
第2个图形中★的个数是4+2=6个，
第3个图形中★的个数是4+2×2=8个，
第4个图形中★的个数是4+2×3=10个，
…
∴第n个图形中★的个数是4+2（n-1）=2n+2个．
故答案为：2n+2．
点评 此题考查图形的变化规律，找出图形之间的联系，得出数字的运算规律，利用规律解决问题．
练习册系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
20．如果把分式$\frac{x+y}{2y}$中的x、y的值都扩大2倍，那么分式的值（ ）
| A． | 扩大2倍 | B． | 扩大6倍 | C． | 扩大3倍 | D． | 不变 |
1．设边长为2a的正方形的中心A在直线l上，它的一组对边垂直于直线l，半径为r的圆的圆心O在直线l上运动，A、O两点之间的距离为d．
（1）如图①，当r＜a时，填表：
（2）如图②，⊙O与正方形有5个公共点B、C、D、E、F，求此时r与a之间的数量关系．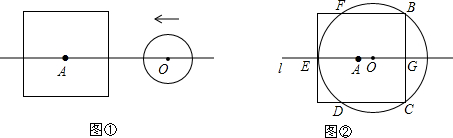
（3）由（1）可知，d、a、r之间的数量关系和⊙O的与正方形的公共点个数密切相关，当r=a时，请根据d、a、r之间的数量关系，判断⊙O与正方形的公共点个数．
（4）当r与a之间满足（2）中的数量关系，⊙O与正方形的公共点个数为0，1，2，5或8．
（1）如图①，当r＜a时，填表：
| d，a，r之间的关系 | ⊙O与正方形的公共点个数 |
| d＞a+r | 0 |
| d=a+r | 1 |
| a-r＜d＜a+r | 2 |
| d=a-r | 1 |
| 0≤d＜a-r | 0 |
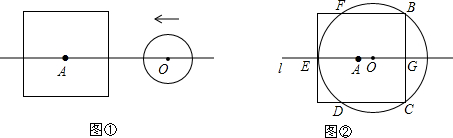
（3）由（1）可知，d、a、r之间的数量关系和⊙O的与正方形的公共点个数密切相关，当r=a时，请根据d、a、r之间的数量关系，判断⊙O与正方形的公共点个数．
（4）当r与a之间满足（2）中的数量关系，⊙O与正方形的公共点个数为0，1，2，5或8．
15．当关于x的方程2x-1=ax+2的解为x=-1时，那么a的值为（ ）
| A． | -1 | B． | -2 | C． | -5 | D． | 5 |
已知：如图，△ABO是等边三角形，CD∥AB，分别交AO、BO的延长线于点C、D．求证：△OCD是等边三角形．
20．已知抛物线y=x2-x-2与x轴的一个交点为（m，0），则代数式m2-m+2013的值为（ ）
| A． | 2013 | B． | 2014 | C． | 2015 | D． | 2016 |