题目内容
1.已知直角三角形的两直角边a=$\sqrt{6}$-$\sqrt{2}$,b=$\sqrt{6}$+$\sqrt{2}$,求这个直角三角形的周长和面积.分析 根据三角形的面积等于两直角边积的一半,再利用已知两直角边长,用勾股定理求斜边,得出三角形的周长.
解答 解:直角三角形的斜边长为:$\sqrt{(\sqrt{6}-\sqrt{2})^{2}+(\sqrt{6}+\sqrt{2})^{2}}$=2$\sqrt{2}$,
周长为:($\sqrt{6}$-$\sqrt{2}$)+($\sqrt{6}$+$\sqrt{2}$)+2$\sqrt{2}$=2($\sqrt{6}$+$\sqrt{2}$)(cm);
直角三角形的面积为:$\frac{1}{2}$($\sqrt{6}$-$\sqrt{2}$)×($\sqrt{6}$+$\sqrt{2}$)=2(cm2).
点评 本题考查了二次根式与三角形边长,面积的综合运用.熟练掌握勾股定理,平方差公式在计算中的作用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
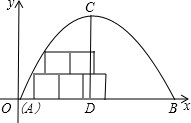 如图,某地下室横截面呈抛物线形,已知跨度AB=6m,最高点C到地面的距离CD=3m.
如图,某地下室横截面呈抛物线形,已知跨度AB=6m,最高点C到地面的距离CD=3m.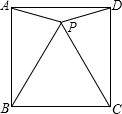 已知P是正方形ABCD内一点,△PBC是等边三角形,若△PAD的外接圆半径是a,求正方形ABCD的边长.
已知P是正方形ABCD内一点,△PBC是等边三角形,若△PAD的外接圆半径是a,求正方形ABCD的边长.