题目内容
(1)如图1矩形ABCD中,AB=8,AD=5,M为AB中点,则S阴影=,S矩形ABCD=.
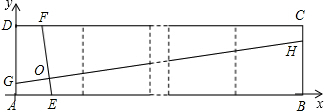
(2)如图2,在直角梯形ABCD中,AD⊥AB,BC⊥BA,AB=8,BC=4,AD=5,M为AB中点,S阴影=,S梯形ABCD=.
(3)如图3在平行四边形ABCD中,∠A=120°,∠B=60°,AB=8,AB的中点为M,AD=5,S阴影=,S四边形ABCD=.
解决问题:如图4有一四边形菜地ABCD,其中AD∥BC,在AB的中点M处有一口井,现要将这块地等分给两家,且都能用井浇地,请你设计方案并说明理由.
解:(1)S阴影=2× ×4×5=20,S矩形ABCD=5×8=40;
×4×5=20,S矩形ABCD=5×8=40;
(2)S阴影=4×4÷2+4×5÷2=18,S梯形ABCD=(4+5)×8÷2=36;
(3)作CE⊥AB,交AB于E.
∵BC=AD=5,∠B=60°,
∴AE=sin60°×BC= .
.
S阴影= ×8×
×8× =10
=10 ,S四边形ABCD=8×
,S四边形ABCD=8× =20
=20 .
.
解决问题方案:连接CM,DM,则S△CMD= S□ABCD.把△CMD分给一家,其他部分分给另外一家即可.
S□ABCD.把△CMD分给一家,其他部分分给另外一家即可.
理由:
过M作ME⊥EB于E延长EM交DA于F.
∵AD∥BC,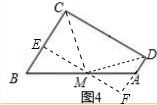
∴MF⊥AD,∠B=∠1.
又∵M为BA中点,
∴BM=MA.
∴△BEM≌△AFM.
∴EM=MF= EF.
EF.
S△CBM+S△DAM= BC•EM+
BC•EM+ AD•MF
AD•MF
= BC×
BC× EF+
EF+ AD×
AD× EF
EF
= (BC+AD)•EF=
(BC+AD)•EF= S?ABCD.
S?ABCD.
∴S△CMD= S?ABCD.
S?ABCD.
分析:(1)根据三角形的面积公式和矩形面积公式计算;
(2)根据三角形的面积公式和梯形面积公式计算;
(3)先求平行四边形AB上的高,再求面积;
(4)有前3题客得规律,连接CM,DM即可.
点评:此题是一道探求规律题,由矩形、梯形、平行四边形的面积计算得出规律,对四边形菜地ABCD即可迎刃而解.

练习册系列答案
相关题目
如图矩形ABCD纸片,我们按如下步骤操作:(1)以过点A的直线为折痕,折叠纸片,使点B落在AD上,折痕与BC交于点E;(2)将纸片展开后,再次折叠纸片,以过点E所在的直线为折痕,使点A落在BC或BC的延长线上,折痕EF交直线AD或直线AB于F,则∠AFE的值为( )


| A、22.5° | B、67.5° | C、22.5°或67.5° | D、45°或135° |
 如图矩形ABCD中AB=8,AD=6,将矩形ABCD在直线l上按顺时针方向转动三次,每次转动90°,则顶点A经过的路线长为
如图矩形ABCD中AB=8,AD=6,将矩形ABCD在直线l上按顺时针方向转动三次,每次转动90°,则顶点A经过的路线长为 如图矩形ABCD中长AB=6、宽AD=2,将矩形ABCD绕A逆时针旋转90°到矩形AB′C′D′,E是AB′的中点,若双曲线
如图矩形ABCD中长AB=6、宽AD=2,将矩形ABCD绕A逆时针旋转90°到矩形AB′C′D′,E是AB′的中点,若双曲线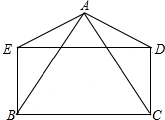 (2013•南通)如图,AB=AC,AD=AE,DE=BC,且∠BAD=∠CAE.
(2013•南通)如图,AB=AC,AD=AE,DE=BC,且∠BAD=∠CAE.