Question

【题目】“我们应该讨论一般化、特殊化和类比这些过程本身，他们是获得发现的伟大源泉”——乔治·波利亚．

（1）观察猜想

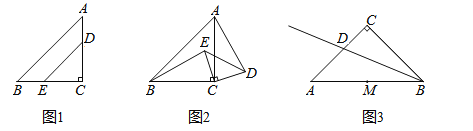
如图1，在△ABC中，CA=CB，．点D在AC上，点E在BC上，且CD=CE．则BE与AD的数量关系是______，直线BE与直线AD的位置关系是______；

（2）拓展探究

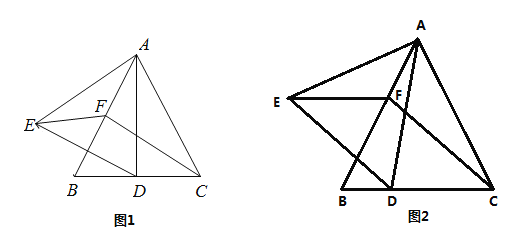
如图2，在△ABC和△CDE中，CA=CB，CD=CE，．则BE与AD的数量关系怎样？直线BE与直线AD的位置关系怎样？请说明理由；

（3）解决问题

如图3，在△ABC中，CA=CB，，BD是△ABC的角平分线，点M是AB的中点．点P在射线BD上，连接PM，以点M为中心，将PM逆时针旋转90°，得到线段MN，请直接写出点A，P，N在同一条直线上时的值．

Answer 1

【答案】（1）；（2），理由见解析；（3）

【解析】

（1）利用等量线段相减的关系得到BE=AD；由直线BE与直线AD的夹角得BE⊥AD；

（2）先利用SAS证明，由此得到，再根据三角形的内角和及对顶角相等的性质得到，由此证得；

（3）分两种情况，连接CP，证明△AMN≌△CMP，即可求出∠CPM=∠ANM，得到答案.

（1）

∵CA=CB,CD=CE,

∴CA-CD=CB-CE,

∴BE=AD；

∵直线BE与直线AD的夹角，

∴BE⊥AD；

故答案为：BE=AD，；

（2）BE=AD，；

设直线交于点.

∵，

，

.

.

.

,

.

即；

（3）如图①，连接CM，

∵CA=CB，，

∴△ABC是等腰直角三角形，

∵M是AB的中点，

∴CM=AM=BM,∠AMC=90，

由旋转得：MN=MP,∠PMN=90，

∴∠AMN=∠CMP,∠MNP=∠MPN=45，

∴△AMN≌△CMP，

∴∠CPM=∠ANM=180-45=135；

如图②连接CM，

∵CM=AM，∠AMN=∠CMP， MN=MP，

∴△AMN≌△CMP，

∴∠CPM=∠ANM=45.