题目内容
已知x+y+z=0,求
+
+
的值.
| x2 |
| 2x2+yz |
| y2 |
| 2y2+zx |
| z2 |
| 2z2+xy |
考点:对称式和轮换对称式
专题:计算题
分析:根据已知条件,将代数式变形为:2x2+yz=-(x-y)(z-x),2y2+zx=-(x-y)(y-z),2z2+xy=-(z-x)(y-z),将上述三个变形结果分别代入所给的代数式中,化简、变形,运算、求值,即可解决问题.
解答:解:∵x+y+z=0,
∴x=-y-z,
2x2+yz=x2+x2+yz=x2+x(-y-z)+yz
=x2-xy-xz+yz=x(x-y)-z(x-y)
=-(x-y)(z-x);
同理可得:2y2+zx=-(x-y)(y-z),
2z2+xy=-(z-x)(y-z),
∴原式
=
+
+
=
∵-x2(y-z)-y2(z-x)-z2(x-y)
=-x2y+x2z-y2z+xy2-xz2+yz2
=-xy(x-y)+z(x+y)(x-y)-z2(x-y)
=(x-y)(-xy+zx+zy-z2)
=(x-y)[x(z-y)-z(z-y)]
=-(x-y)(y-z)(z-x),
∴原式=
=-1.
∴x=-y-z,
2x2+yz=x2+x2+yz=x2+x(-y-z)+yz
=x2-xy-xz+yz=x(x-y)-z(x-y)
=-(x-y)(z-x);
同理可得:2y2+zx=-(x-y)(y-z),
2z2+xy=-(z-x)(y-z),
∴原式
=
| -x2 |
| (x-y)(z-x) |
| -y2 |
| (x-y)(y-z) |
| -z2 |
| (z-x)(y-z) |
=
| -x2(y-z)-y2(z-x)-z2(x-y) |
| (x-y)(y-z)(z-x) |
∵-x2(y-z)-y2(z-x)-z2(x-y)
=-x2y+x2z-y2z+xy2-xz2+yz2
=-xy(x-y)+z(x+y)(x-y)-z2(x-y)
=(x-y)(-xy+zx+zy-z2)
=(x-y)[x(z-y)-z(z-y)]
=-(x-y)(y-z)(z-x),
∴原式=
| -(x-y)(y-z)(z-x) |
| (x-y)(y-z)(z-x) |
点评:该题考查了对称式和轮换对称式的化简与求值问题;解题的关键是深刻把握所给代数式的结构特点,灵活运用有关公式将所给的代数式变形、化简、计算、求值.

练习册系列答案
相关题目
化简
的结果是( )
| a-|a| |
| |a| |
| A、0或-2 | B、-2 |
| C、0或2 | D、2 |
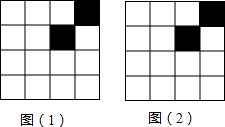 如图,在“4×4”正方形网格中,已有2个小正形被涂黑.请你分别在下面2张图中再将若干个空白的小正方形涂黑,使得涂黑的图形成为轴对称图形.(图(1)要求只有1条对称轴,图(2)要求只有2条对称轴).
如图,在“4×4”正方形网格中,已有2个小正形被涂黑.请你分别在下面2张图中再将若干个空白的小正方形涂黑,使得涂黑的图形成为轴对称图形.(图(1)要求只有1条对称轴,图(2)要求只有2条对称轴).