题目内容
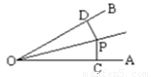
 如图,P在∠AOB的平分线上,若PD=PE,须添加一个条件:________;(只填写一个)
如图,P在∠AOB的平分线上,若PD=PE,须添加一个条件:________;(只填写一个)
①PD⊥OA,PE⊥OB或②∠ODP=∠OEP或③∠OPE=∠ODE或④OD=OE
分析:由P在∠AOB的平分线上,利用角平分线的性质与全等三角形的判定与性质,即可求得答案.
解答:∵P在∠AOB的平分线上,
∴若①PD⊥OA,PE⊥OB,
∴PD=PE;
若 ②∠ODP=∠OEP,
在△OPD和△OPE中,
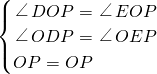 ,
,
∴△OPD≌△OPE(AAS),
∴PD=PE;
若③∠OPE=∠ODE或 ④OD=OE;
可得△OPD≌△OPE(AAS),
∴PD=PE.
故答案为:此题答案不唯一,如①PD⊥OA,PE⊥OB或②∠ODP=∠OEP或③∠OPE=∠ODE或④OD=OE.
点评:此题考查了角平分线的性质以及全等三角形的判定与性质.此题难度不大,属于开放题,注意角的平分线上的点到角的两边的距离相等.
分析:由P在∠AOB的平分线上,利用角平分线的性质与全等三角形的判定与性质,即可求得答案.
解答:∵P在∠AOB的平分线上,
∴若①PD⊥OA,PE⊥OB,
∴PD=PE;
若 ②∠ODP=∠OEP,
在△OPD和△OPE中,
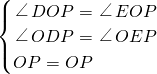 ,
,∴△OPD≌△OPE(AAS),
∴PD=PE;
若③∠OPE=∠ODE或 ④OD=OE;
可得△OPD≌△OPE(AAS),
∴PD=PE.
故答案为:此题答案不唯一,如①PD⊥OA,PE⊥OB或②∠ODP=∠OEP或③∠OPE=∠ODE或④OD=OE.
点评:此题考查了角平分线的性质以及全等三角形的判定与性质.此题难度不大,属于开放题,注意角的平分线上的点到角的两边的距离相等.

练习册系列答案
相关题目
 如图,P在∠AOB的内部,PC⊥AO于C,PD⊥OB于D,PD=PC,当∠AOP=x度,∠BOP=(110-4x)度时,∠AOP=
如图,P在∠AOB的内部,PC⊥AO于C,PD⊥OB于D,PD=PC,当∠AOP=x度,∠BOP=(110-4x)度时,∠AOP= 如图,P在∠AOB的平分线上,若PD=PE,须添加一个条件:
如图,P在∠AOB的平分线上,若PD=PE,须添加一个条件: 如图,P在∠AOB的内部,PC⊥AO于C,PD⊥OB于D,PD=PC,当∠AOP=(2x-10)度,∠BOP=(x+5)度时,∠AOB=
如图,P在∠AOB的内部,PC⊥AO于C,PD⊥OB于D,PD=PC,当∠AOP=(2x-10)度,∠BOP=(x+5)度时,∠AOB=