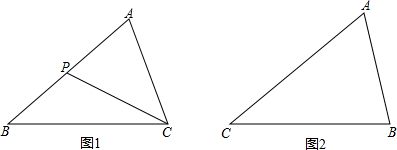
题目内容
在△ABC中,M是边AC的中点,P为AM上一点,过P作PK∥AB交BM于X,交BC于K.若PX=2,XK=3,则AB=________.
8
分析:根据平行四边形的性质以及平行线分线段成比例定理得出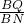 =
= =
=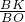 =
=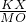 ,再利用MO=NO即可得出KQ=XK=3,求出AB即可.
,再利用MO=NO即可得出KQ=XK=3,求出AB即可.
解答: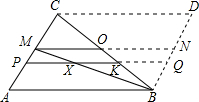 解:以BC为对角线作平行四边形ABDC,延长PK交BD于Q,过M作AB的平行线交CB于O,交BD于N,则AB=QP=NM,
解:以BC为对角线作平行四边形ABDC,延长PK交BD于Q,过M作AB的平行线交CB于O,交BD于N,则AB=QP=NM,
∴CO=BO,O是平行四边形ABDC的中心,
∴MO=NO,
∵PQ∥MN,
∴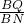 =
= =
=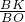 =
=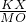 ,
,
∵MO=NO,
∴KQ=XK=3,
∴AB=PX+XK+KQ=2+3+3=8.
故答案为:8.
另一种解法:
解:∵PK‖AB,
∴ =
= ,
,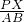 =
= ,
,
∵PK=PX+XK=2+3=5,
PC=PM+MC,AC=2MC=2AM
∴ =
=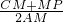 =
=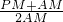 =
=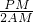 +
+ ,
,
∴MP= ,
,
 =
= ,
,
∴ =
=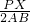 +
+ ,
,
 =
=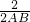 +
+ ,
,
 -
- =
= ,
,
 =
= ,
,
∴AB=8.
故答案为:8.
点评:此题主要考查了平行四边形的性质以及平行线分线段成比例定理等知识,正确作出辅助线得出KQ=XK是解题关键.
分析:根据平行四边形的性质以及平行线分线段成比例定理得出
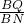 =
= =
=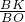 =
=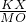 ,再利用MO=NO即可得出KQ=XK=3,求出AB即可.
,再利用MO=NO即可得出KQ=XK=3,求出AB即可.解答:
 解:以BC为对角线作平行四边形ABDC,延长PK交BD于Q,过M作AB的平行线交CB于O,交BD于N,则AB=QP=NM,
解:以BC为对角线作平行四边形ABDC,延长PK交BD于Q,过M作AB的平行线交CB于O,交BD于N,则AB=QP=NM,∴CO=BO,O是平行四边形ABDC的中心,
∴MO=NO,
∵PQ∥MN,
∴
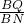 =
= =
=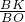 =
=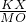 ,
,∵MO=NO,
∴KQ=XK=3,
∴AB=PX+XK+KQ=2+3+3=8.
故答案为:8.
另一种解法:
解:∵PK‖AB,
∴
 =
= ,
,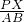 =
= ,
,∵PK=PX+XK=2+3=5,
PC=PM+MC,AC=2MC=2AM
∴
 =
=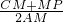 =
=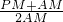 =
=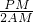 +
+ ,
,∴MP=
 ,
, =
= ,
,∴
 =
=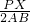 +
+ ,
, =
=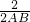 +
+ ,
, -
- =
= ,
, =
= ,
,∴AB=8.
故答案为:8.
点评:此题主要考查了平行四边形的性质以及平行线分线段成比例定理等知识,正确作出辅助线得出KQ=XK是解题关键.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
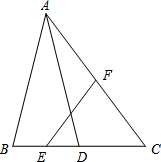 (2013•闵行区三模)已知:如图,在△ABC中,D是边BC的中点,E、F分别是BD、AC的中点,且AB=AD,AC=10,sinC=
(2013•闵行区三模)已知:如图,在△ABC中,D是边BC的中点,E、F分别是BD、AC的中点,且AB=AD,AC=10,sinC= 如图,在△ABC中,M是边BC的中点,AN平分∠BAC,BN⊥AN,若AB=14cm,AC=19cm,则MN的长度是
如图,在△ABC中,M是边BC的中点,AN平分∠BAC,BN⊥AN,若AB=14cm,AC=19cm,则MN的长度是 如图,在△ABC中,D是边AC的中点,点E在边AB上,且AE=2BE,BD与CE相交于点F,若△BEF的面积等于1,求△ABC和△ADE的面积.
如图,在△ABC中,D是边AC的中点,点E在边AB上,且AE=2BE,BD与CE相交于点F,若△BEF的面积等于1,求△ABC和△ADE的面积.