题目内容
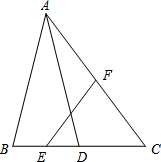 (2013•闵行区三模)已知:如图,在△ABC中,D是边BC的中点,E、F分别是BD、AC的中点,且AB=AD,AC=10,sinC=
(2013•闵行区三模)已知:如图,在△ABC中,D是边BC的中点,E、F分别是BD、AC的中点,且AB=AD,AC=10,sinC=| 4 | 5 |
(1)线段EF的长;
(2)∠B的余弦值.
分析:(1)连接AE,根据AB=AD,E为BD中点,可证得AE⊥BD,然后根据F为AC的中点,可得EF=
AC,即可求出EF的长度;
(2)在Rt△AEC中,根据AC=10,sinC=
,求出AE、EC的长度,然后根据D、E分别为BC、BD的中点,求出BE的长度,根据勾股定理求出AB的长度,继而可求得∠B的余弦值.
| 1 |
| 2 |
(2)在Rt△AEC中,根据AC=10,sinC=
| 4 |
| 5 |
解答:解:(1)连接AE.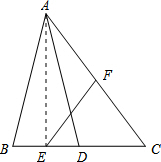
∵AB=AD,E为BD的中点,
∴AE⊥BD,即得∠AEC=90°.
又∵F是AC的中点,AC=10,
∴EF=
AC=5;
(2)在Rt△AEC中,
∵sinC=
=
,
∴AE=
AC=
×10=8,
∴CE=
=
=6,
∵D是边BC的中点,
∴BD=CD,
又∵E为BD的中点,
∴BE=ED=
BD,
∵CE=CD+ED=2BE+BE=6,
∴BE=2,
∴AB=
=
=2
,
∴cosB=
=
=
.

∵AB=AD,E为BD的中点,
∴AE⊥BD,即得∠AEC=90°.
又∵F是AC的中点,AC=10,
∴EF=
| 1 |
| 2 |
(2)在Rt△AEC中,
∵sinC=
| AE |
| AC |
| 4 |
| 5 |
∴AE=
| 4 |
| 5 |
| 4 |
| 5 |
∴CE=
| AC2-AE2 |
| 102-82 |
∵D是边BC的中点,
∴BD=CD,
又∵E为BD的中点,
∴BE=ED=
| 1 |
| 2 |
∵CE=CD+ED=2BE+BE=6,
∴BE=2,
∴AB=
| AE2+BE2 |
| 82+22 |
| 17 |
∴cosB=
| BE |
| AB |
| 2 | ||
2
|
| ||
| 17 |
点评:本题考查了解直角三角形,解答本题的关键是掌握直角三角形斜边上的中线等于斜边的一半以及勾股定理的应用.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
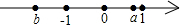 (2013•闵行区三模)已知实数a、b在数轴上的位置如图所示,那么下列等式成立的是( )
(2013•闵行区三模)已知实数a、b在数轴上的位置如图所示,那么下列等式成立的是( )