题目内容
2.填空:(1)已知DE∥BC,则△ADE∽△ABC;
(2)已知∠A=∠D,则$\frac{CD}{AC}$=$\frac{CE}{BC}$=$\frac{DE}{AB}$(填边长比例关系);
(3)已知∠DAB=∠CAE,AB•AD=AE•AC,则∠ADE=∠C;
(4)已知∠ABP=CDP,则PA•CD═PC•AB;
(5)已知:∠ABC=90°,∠ACB=30°,AD=2AC,CD=2BC,则∠D=30°.

分析 根据相似三角形的判定和性质定理即可得到结论.
解答 解:(1)已知DE∥BC,则△ADE∽△ABC;
(2)已知∠A=∠D,则$\frac{CD}{AC}$=$\frac{CE}{BC}$=$\frac{DE}{AB}$,(填边长比例关系);
(3)已知∠DAB=∠CAE,AB•AD=AE•AC,则∠ADE=∠C;
(4)已知∠ABP=∠CDP,则PA•CD═PC•AB;
(5)已知:∠ABC=90°,∠ACB=30°,AD=2AC,CD=2BC,则∠D=30°.
故答案为:△ADE∽△ABC,$\frac{CD}{AC}$,$\frac{CE}{BC}$,$\frac{DE}{AB}$,∠C,PC•AB,30°.
点评 本题考查了相似三角形的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 在梯形ABCD中,AH∥DC,E是AB的中点,直线ED分别与对角线AC和BC的延长线交于M,N点.求证:MD•NE=ND•ME.
在梯形ABCD中,AH∥DC,E是AB的中点,直线ED分别与对角线AC和BC的延长线交于M,N点.求证:MD•NE=ND•ME.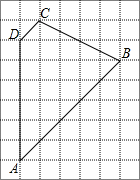 如图所示,图中小正方形的边长为1,试求图中梯形ABCD的面积,你有哪些方法?与同伴进行交流.
如图所示,图中小正方形的边长为1,试求图中梯形ABCD的面积,你有哪些方法?与同伴进行交流. 如图,抛物线y=-$\frac{3}{8}$x2+$\frac{3}{4}$x+3与x轴交于A、B两点,与y轴交于点C,在y轴上是否存在点M使△ACM为等腰三角形?若存在,求出所有满足条件的M点坐标;若不存在,请说明理由.
如图,抛物线y=-$\frac{3}{8}$x2+$\frac{3}{4}$x+3与x轴交于A、B两点,与y轴交于点C,在y轴上是否存在点M使△ACM为等腰三角形?若存在,求出所有满足条件的M点坐标;若不存在,请说明理由. 如图,△ABC中,∠ACB=90°,AC=BC,AD是中线,点E与点C关于AD对称,CE交AD于F,连接BE.
如图,△ABC中,∠ACB=90°,AC=BC,AD是中线,点E与点C关于AD对称,CE交AD于F,连接BE. ,反比例函数
,反比例函数 (k≠0,x>0)经过点C.则k的值等于( )
(k≠0,x>0)经过点C.则k的值等于( )