题目内容
16. 哈六十九中学校要在教学楼后面的空地上用40米长的竹篱笆围成一个矩形ABCD生物园(如图所示),设矩形的边AB(AB>BC)为x米,面积为y平方米.
哈六十九中学校要在教学楼后面的空地上用40米长的竹篱笆围成一个矩形ABCD生物园(如图所示),设矩形的边AB(AB>BC)为x米,面积为y平方米.(1)求y与x之间的函数关系式(不要求写出x的取值范围);
(2)当x为多少米时,y有最大值?并求出这个最大值.
[参考公式:二次函数y=ax2+bx+c(a≠0),当x=$-\frac{b}{2a}$时,y最大(小)值=$\frac{{4ac-{b^2}}}{4a}$].
分析 (1)矩形的边AB(AB>BC)为x米,面积为y平方米,根据矩形面积公式“面积=长×宽”列出函数的关系式;
(2)求出顶点坐标,根据二次函数的性质即可解决.
解答 解:(1)矩形的边AB(AB>BC)为x米,面积为y平方米,则
y=x(20-x)--x2+20x;
(2)y=-x2+20x=-(x-10)2+100
∴当x=10米时,y有最大值,最大值为100m2.
点评 本题考查了二次函数的应用.关键是根据矩形面积公式列出函数式,利用二次函数的性质解题.

练习册系列答案
相关题目
7.某市2010年平均房价为每平方米4000元.连续两年增长后,2012年平均房价达到每平方米5500元.设这两年平均房价年平均增长率为x,根据题意,下面所列方程正确的是( )
| A. | 5500(1+x)2=4000 | B. | 5500(1-x)2=4000 | C. | 4000(1-x)2=5500 | D. | 4000(1+x)2=5500 |
8.下列二次根式中,最简二次根式是( )
| A. | $\sqrt{12}$ | B. | $\sqrt{{x}^{2}+2xy-{y}^{2}}$ | C. | $\sqrt{2{x}^{3}}$ | D. | $\sqrt{\frac{x}{2}}$ |

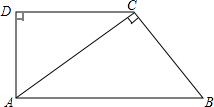 如图,在直角梯形ABCD中,AB∥DC,∠D=90°,AC⊥BC,AB=10cm,BC=6cm,
如图,在直角梯形ABCD中,AB∥DC,∠D=90°,AC⊥BC,AB=10cm,BC=6cm,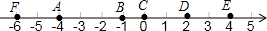 在如图所示的数轴上有A、B、C、D、E、F六个点,按要求完成下列各小题.
在如图所示的数轴上有A、B、C、D、E、F六个点,按要求完成下列各小题. 如图,在平行四边形ABCD中,AD=5,AB=3,BE平分∠ABC,则DE=2.
如图,在平行四边形ABCD中,AD=5,AB=3,BE平分∠ABC,则DE=2.