题目内容
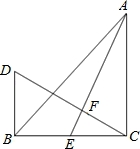
如图,在△ABC中,∠ACB=90°,AC=BC,AE是BC边的中线,过点C作CF⊥AE,垂足为点F,过点 B作BD⊥BC交CF的延长线于点D.
B作BD⊥BC交CF的延长线于点D.
(1)试说明AE=CD;
(2)若AC=10cm,求BD的长.
【考点】全等三角形的判定与性质.
【专题】几何综合题.
【分析】(1)证两条线段相等,通常用全等,本题中的AE和CD分别在三角形AEC和三角形CDB中,在这两个三角形中,已经有一组边相等,一组角相等了,因此只需再找一组角即可利用角角边进行解答.
(2)由(1)得BD=EC= BC=
BC= AC,且AC=10cm,即可求出BD的长.
AC,且AC=10cm,即可求出BD的长.
【解答】(1)证明:∵DB⊥BC,CF⊥AE,
∴∠DCB+∠D=∠DCB+∠AEC=90°.
∴∠D=∠AEC.
又∵∠DBC=∠ECA=90°,
且BC=CA,
∴△DBC≌△ECA(AAS).
∴AE=CD.
(2)解:由(1)得AE=CD,AC=BC,
∴Rt△CDB≌Rt△AEC(HL)
∴BD=EC= BC=
BC= AC,且AC=10cm.
AC,且AC=10cm.
∴BD=5cm.
【点评】三角形全等的判定是中考的热点,一般以考查三角形全等的方法为主,判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.

练习册系列答案
相关题目
 .
. +|1﹣
+|1﹣ |﹣(π﹣1)0.
|﹣(π﹣1)0.
 )
)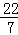 ;③3.33333…;④π;⑤2.020020002…(每两个2之间依据增加一个0)
;③3.33333…;④π;⑤2.020020002…(每两个2之间依据增加一个0)