题目内容
14.在平面直角坐标系中,已知A(-3,0),B(0,4),C(1,m),当△ABC是直角三角形时,m的值为-3或$\frac{13}{4}$或2.分析 分三种情况:①A是直角顶点;②B是直角顶点;③C是直角顶点;进行讨论可求当△ABC是直角三角形时,m的值.
解答 解:①A是直角顶点,
(-3-0)2+(0-4)2+(-3-1)2+(0-m)2=(0-1)2+(m-4)2,
解得m=-3;
②B是直角顶点,
(-3-0)2+(0-4)2+(0-1)2+(m-4)2=(-3-1)2+(0-m)2,
解得m=$\frac{13}{4}$;
③C是直角顶点,
(-3-1)2+(0-m)2+(0-1)2+(m-4)2=(-3-0)2+(0-4)2,
解得m=2.
故当△ABC是直角三角形时,m的值为-3或$\frac{13}{4}$或2.
故答案为:-3或$\frac{13}{4}$或2.
点评 考查了勾股定理,用到的知识点为:若△ABC是直角三角形,则它的任意一个顶点都有可能为直角顶点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案
相关题目
4.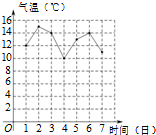 如图是我市4月1日至7日一周内“日平均气温变化统计图”,在这组数据中,众数和中位数分别是( )
如图是我市4月1日至7日一周内“日平均气温变化统计图”,在这组数据中,众数和中位数分别是( )
 如图是我市4月1日至7日一周内“日平均气温变化统计图”,在这组数据中,众数和中位数分别是( )
如图是我市4月1日至7日一周内“日平均气温变化统计图”,在这组数据中,众数和中位数分别是( )| A. | 13,13 | B. | 14,10 | C. | 14,13 | D. | 13,14 |
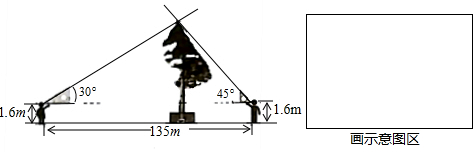
 已知:∠B+∠C=90°,AD∥BC,M,N分别是AD、BC中点,求证:MN=$\frac{1}{2}$(BC-AD).
已知:∠B+∠C=90°,AD∥BC,M,N分别是AD、BC中点,求证:MN=$\frac{1}{2}$(BC-AD).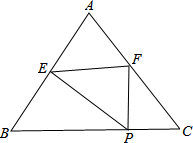 如图,已知,等腰△ABC中,AB=AC=5,BC=6,点P在BC上(与B,C不重合),作PE⊥AB,垂足是E,PF⊥BC,交AC于F,设PC=x,△PEF面积为y.
如图,已知,等腰△ABC中,AB=AC=5,BC=6,点P在BC上(与B,C不重合),作PE⊥AB,垂足是E,PF⊥BC,交AC于F,设PC=x,△PEF面积为y.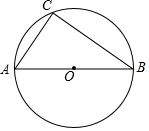 已知:如图,已知⊙O是△ABC的外接圆,AB为⊙O的直径,AC=6cm,BC=8cm.
已知:如图,已知⊙O是△ABC的外接圆,AB为⊙O的直径,AC=6cm,BC=8cm.