题目内容
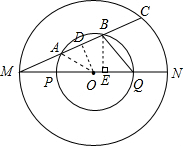
 如图,在以O为圆心的两个同心圆中,MN为大圆的直径,交小圆于点P、Q,大圆的弦MC交小圆于点A、B.若OM=2,OP=1,MA=AB=BC,则△MBQ的面积为________.
如图,在以O为圆心的两个同心圆中,MN为大圆的直径,交小圆于点P、Q,大圆的弦MC交小圆于点A、B.若OM=2,OP=1,MA=AB=BC,则△MBQ的面积为________.

分析:首先过O点作OD⊥AB,垂足为D,连接OA,设OD=x,AD=y,利用勾股定理和垂径定理求出x和y的值,继而求出sin∠MDO的值,然后过B点作BE⊥MQ,垂足为E,在Rt△MEB中,sin∠BME=sin∠MDO,求出BE的值,利用三角形的面积公式求出△MBQ的面积.
解答:过O点作OD⊥AB,垂足为D,连接OA,
设OD=x,AD=y,
∵O是圆心,MC是圆的一条弦,OD⊥AB,
∴AD=DB=
 AB,MD=CD=
AB,MD=CD= MC,
MC,∵MA=AB=BC,
∴MA=2AD,
在Rt△ADO中,AD2+OD2=OA2,
即y2+x2=1…①,
在Rt△MDO中,OD2+MD2=MO2,
即x2+9y2=4…②,
联立①②解得x=
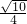 ,y=
,y= ,
,在Rt△MDO中,sin∠MDO=
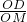 =
=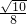 ,
,过B点作BE⊥MQ,垂足为E,
在Rt△MEB中,sin∠BME=
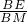 =
=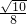 ,
,解得BE=
 ,
,S△BMQ=
 MQ•BE=
MQ•BE= ×3×
×3× =
= ,
,故答案为
 .
.点评:本题主要考查垂径定理和勾股定理的知识点,解答本题的关键是添加辅助线,利用辅助线构造成直角三角形进行解题,此题是一道比较典型的试题,请同学们注意.

练习册系列答案
相关题目
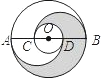 如图,在以O为圆心的两个同心圆中,大圆的直径AB交小圆于C、D两点,AC=CD=DB,分别以C、D为圆心,以CD为半径作圆.若AB=6cm,则图中阴影部分的面积为
如图,在以O为圆心的两个同心圆中,大圆的直径AB交小圆于C、D两点,AC=CD=DB,分别以C、D为圆心,以CD为半径作圆.若AB=6cm,则图中阴影部分的面积为 9、如图,在以O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,点P为切点,已知AB=8,大圆半径为5,则小圆半径为( )
9、如图,在以O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,点P为切点,已知AB=8,大圆半径为5,则小圆半径为( ) (2006•静安区二模)如图,在以O为圆心的两个同心圆中,小圆的半径为1,AB与小圆相切于点A,与大圆相交于B,大圆的弦BC⊥AB,过点C作大圆的切线交AB的延长线于D,OC交小圆于E
(2006•静安区二模)如图,在以O为圆心的两个同心圆中,小圆的半径为1,AB与小圆相切于点A,与大圆相交于B,大圆的弦BC⊥AB,过点C作大圆的切线交AB的延长线于D,OC交小圆于E 如图,在以O为圆心的两个同心圆中,MN为大圆的直径,交小圆于点P、Q,大圆的弦MC交小圆于点A、B.若OM=2,OP=1,MA=AB=BC,则△MBQ的面积为
如图,在以O为圆心的两个同心圆中,MN为大圆的直径,交小圆于点P、Q,大圆的弦MC交小圆于点A、B.若OM=2,OP=1,MA=AB=BC,则△MBQ的面积为 如图,在以O为圆心的两个同心圆中,大圆的弦AB与小圆相切于点C,若大圆的半径为5cm,小圆的半径为3cm,则弦AB的长为( )
如图,在以O为圆心的两个同心圆中,大圆的弦AB与小圆相切于点C,若大圆的半径为5cm,小圆的半径为3cm,则弦AB的长为( )