题目内容
 如图,已知∠BAC=130°,AB=AC,AC的垂直平分线交BC于点D,则∠ADB=
如图,已知∠BAC=130°,AB=AC,AC的垂直平分线交BC于点D,则∠ADB=50
50
度.分析:根据线段垂直平分线上的点到线段两端点的距离相等可得AD=CD,再根据等边对等角可得∠C=∠CAD,∠B=∠C,然后利用三角形内角和定理列式求出∠C,再根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解.
解答:解:∵DE是AC的垂直平分线,
∴AD=CD,
∴∠C=∠CAD,
∵AB=AC,
∴∠B=∠C,
在△ABC中,∠ABC+∠B+∠C=180°,
∴130°+2∠C=180°,
解得∠C=25°,
∴∠ADB=∠CAD+∠C=25°+25°=50°.
故答案为:50.
∴AD=CD,
∴∠C=∠CAD,
∵AB=AC,
∴∠B=∠C,
在△ABC中,∠ABC+∠B+∠C=180°,
∴130°+2∠C=180°,
解得∠C=25°,
∴∠ADB=∠CAD+∠C=25°+25°=50°.
故答案为:50.
点评:本题考查了线段垂直平分线上的点到线段两端点的距离相等的性质,等腰三角形的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记性质并利用三角形的内角和定理列出方程是解题的关键.

练习册系列答案
相关题目
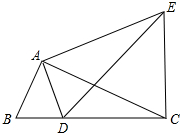 如图,已知∠BAC=90°,△ABC绕点A逆时针旋转得到△ADE,恰好D在BC上,连接CE.
如图,已知∠BAC=90°,△ABC绕点A逆时针旋转得到△ADE,恰好D在BC上,连接CE. 如图,已知∠BAC的平分线与△ABC的边BC和外接圆分别相交于D、E.
如图,已知∠BAC的平分线与△ABC的边BC和外接圆分别相交于D、E. 如图,已知∠BAC=70°,D是△ABC的边BC上的一点,且∠CAD=∠C,∠ADB=80°.求∠B的度数.
如图,已知∠BAC=70°,D是△ABC的边BC上的一点,且∠CAD=∠C,∠ADB=80°.求∠B的度数.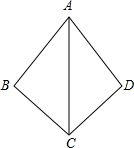 如图,已知∠BAC=∠DAC,要利用“ASA”判定△ABC≌△ADC,则应添加的条件是
如图,已知∠BAC=∠DAC,要利用“ASA”判定△ABC≌△ADC,则应添加的条件是 如图,已知∠BAC=40°,∠DAC=10°,若将△ABC绕点A逆时针旋转
如图,已知∠BAC=40°,∠DAC=10°,若将△ABC绕点A逆时针旋转