题目内容
13.先化简再求值(1)-2y3+(2x3-xyz)-2(x3-xyz),其中x=1,y=-2,z=-3.
(2)已知-xm-2nyn-2与$\frac{1}{3}$x5y4-m是同类项,求(m-2n)2-5(m+n)-2(m-2n)2+m+n的值.
分析 (1)原式去括号合并得到最简结果,把x,y,z的值代入计算即可求出值;
(2)利用同类项的定义求出m与n的值,代入原式计算即可得到结果.
解答 解:(1)原式=-2y3+2x3-xyz-2x3+2xyz=-2y3+xyz,
当x=1,y=-2,z=-3时,原式=16+6=22;
(2)原式=-(m-2n)2-4(m+n),
∵-xm-2nyn-2与$\frac{1}{3}$x5y4-m是同类项,
∴m-2n=5,n-2=4-m,即m+n=6,
则原式=-25-24=-49.
点评 此题考查了整式的加减-化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
4.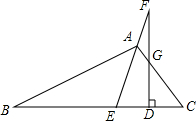 如图,在△ABC中,AE是△ABC的角平分线,在EA的延长线上取一点F,作FD⊥BC于点D,若∠B=36°,∠C=64°,则∠EFD的度数为( )
如图,在△ABC中,AE是△ABC的角平分线,在EA的延长线上取一点F,作FD⊥BC于点D,若∠B=36°,∠C=64°,则∠EFD的度数为( )
 如图,在△ABC中,AE是△ABC的角平分线,在EA的延长线上取一点F,作FD⊥BC于点D,若∠B=36°,∠C=64°,则∠EFD的度数为( )
如图,在△ABC中,AE是△ABC的角平分线,在EA的延长线上取一点F,作FD⊥BC于点D,若∠B=36°,∠C=64°,则∠EFD的度数为( )| A. | 10° | B. | 12° | C. | 14° | D. | 16° |
1.下列说法正确的是( )
| A. | 符号相反的两个数互为相反数 | |
| B. | 一个数的绝对值越大,表示它的点在数轴上越靠右 | |
| C. | 一个数的绝对值越大,表示它的点在数轴上离原点越近 | |
| D. | 当a≠0时,|a|总是大于0 |
18.甲、乙、丙三地的海拔高度分别为50米,-5米和-15米,那么最高的地方比最低的地方高( )
| A. | 35米 | B. | 25米 | C. | 55米 | D. | 65米 |
 如图,在Rt△ABO中,顶点A是双曲线y=$\frac{k}{x}$与直线y=-x+(k+1)在第四象限的交点,AB⊥x轴于B且S△ABO=1.5.
如图,在Rt△ABO中,顶点A是双曲线y=$\frac{k}{x}$与直线y=-x+(k+1)在第四象限的交点,AB⊥x轴于B且S△ABO=1.5.