题目内容
20．如图，A，B，C，D是直线l上的四点，M，N分别是AB，CD的中点，如果MN=a，BC=b，求AD的长．
分析 根据线段的和差，可得（MB+CN）的长，根据线段中点的性质，可得AB与MB的关系，CD与CN的关系，根据线段的和差，可得答案．
解答 解：由线段的和差，得（MB+CN）=MN-BC=a-b，
由M、N分别是AB、CD的中点，得AB=2MB，CD=2CN．
由线段的和差，得AD=AB+BC+CD=（AB+CD）+BC=2（MB+CN）+BC=2×（a-b）+b=2a-b．
点评 本题考查了两点间的距离，利用线段的和差得出（MB+CN）的长，利用线段中点的性质，得出AB=2MB，CD=2CN．
练习册系列答案
举一反三单元同步过关卷系列答案
相关题目
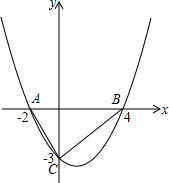如图，二次函数的图象经过A、B、C三点
已知A（1，2），B（m，$\frac{1}{2}$）是双曲线上的点．
如图，A，B，C是同一直线上的三个点，图中共有几条射线？在不增加字母的情况下，能表示出的射线共几条？是哪几条？
如图所示，D是△ABC中BC边的中点，且AB=5，AC=7，请你求AD的取值范围．