题目内容
已知直线y=-x+2与x轴交于点A,与y轴交于B点,一抛物线经过A、B两点,且其对称轴为直线x=12.
(1)求这条抛物线的解析式;
(2)求这条抛物线的顶点坐标;
(3)求这条抛物线与x轴的两交点和与y轴的交点所围成的三角形面积.
(1)求这条抛物线的解析式;
(2)求这条抛物线的顶点坐标;
(3)求这条抛物线与x轴的两交点和与y轴的交点所围成的三角形面积.
考点:待定系数法求二次函数解析式,二次函数的性质,抛物线与x轴的交点
专题:计算题
分析:(1)设抛物线解析式为y=ax2+bx+c(a≠0),把A,B坐标代入得到两个方程,再利用对称轴公式列出方程组,求出a,b,c的值,即可确定出抛物线解析式;
(2)利用顶点坐标公式求出抛物线顶点坐标即可;
(3)求出抛物线与x轴两交点,以及与y轴交点,求出围成的三角形面积即可.
(2)利用顶点坐标公式求出抛物线顶点坐标即可;
(3)求出抛物线与x轴两交点,以及与y轴交点,求出围成的三角形面积即可.
解答:解:(1)设抛物线解析式为y=ax2+bx+c(a≠0),A(2,0),B(0,2),
根据题意得:
,
解得:a=
,b=-
,c=2,
则抛物线解析式为y=
x2-
x+2;
(2)抛物线顶点坐标为(12,-
);
(3)令y=0,得到
x2-
x+2=0,
解得:x=22或2,即A(2,0),C(22,0),
令x=0,得到y=2,即B(0,2),
则S△ABC=
×20×2=20.
根据题意得:
|
解得:a=
| 1 |
| 22 |
| 12 |
| 11 |
则抛物线解析式为y=
| 1 |
| 22 |
| 12 |
| 11 |
(2)抛物线顶点坐标为(12,-
| 50 |
| 11 |
(3)令y=0,得到
| 1 |
| 22 |
| 12 |
| 11 |
解得:x=22或2,即A(2,0),C(22,0),
令x=0,得到y=2,即B(0,2),
则S△ABC=
| 1 |
| 2 |
点评:此题考查了待定系数法求二次函数解析式,二次函数的性质,以及抛物线与x轴的交点,熟练掌握待定系数法是解本题的关键.

练习册系列答案
相关题目
已知⊙O的半径是3,点O到直线l的距离为1,则直线l与⊙O的位置关系是( )
| A、相离 | B、相切 |
| C、相交 | D、无法判断 |
在数轴上表示整数的点称为整数点,某数轴的单位长度是1cm,若在这个数轴上随意画出一条长2015cm的线段AB,则被线段AB盖住的整数有( )
| A、2012个或2013个 |
| B、2013个或2014个 |
| C、2014个或2015个 |
| D、2015个或2016个 |
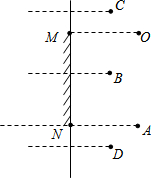 如图所示,一面镜子MN竖直悬挂在墙壁上,人眼O的位置与镜子MN上沿M处于同一水平线. 有四个物体A、B、C、D放在镜子前面,人眼能从镜子看见的物体有
如图所示,一面镜子MN竖直悬挂在墙壁上,人眼O的位置与镜子MN上沿M处于同一水平线. 有四个物体A、B、C、D放在镜子前面,人眼能从镜子看见的物体有