题目内容
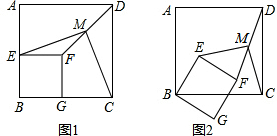
已知:如图1,正方形ABCD和正方形EBGF,点M是线段DF的中点.
(1)试说明线段ME与MC的关系.
(2)如图2,若将上题中正方形EBGF绕点B顺时针旋转α度数(α<90°),其他条件不变,上述结论还正确吗?若正确,请你证明;若不正确,请说明理由.
(1)试说明线段ME与MC的关系.
(2)如图2,若将上题中正方形EBGF绕点B顺时针旋转α度数(α<90°),其他条件不变,上述结论还正确吗?若正确,请你证明;若不正确,请说明理由.

考点:全等三角形的判定与性质,正方形的性质
专题:
分析:(1)延长EM、AD交于点H,连接EC,HC,由条件可以得出△EFM≌△HDM,就可以得出DH=EF,再由正方形的性质就可以得出△EBC≌△HDC,就可以得出△ECH为等腰直角三角形,从而得出结论;
(2)延长EM到H.使MH=ME,连接DH,EC,HC,由条件可以得出△EFM≌△HDM,就可以得出DH=EF,DH∥EF,由正方形EBGF绕点B顺时针旋转α度,就可以得出∠ABE=∠NDH=a,得出∠EBC=∠HDC,就可以得出△EBC≌△HDC,就可以得出△ECH为等腰直角三角形,从而得出结论.
(2)延长EM到H.使MH=ME,连接DH,EC,HC,由条件可以得出△EFM≌△HDM,就可以得出DH=EF,DH∥EF,由正方形EBGF绕点B顺时针旋转α度,就可以得出∠ABE=∠NDH=a,得出∠EBC=∠HDC,就可以得出△EBC≌△HDC,就可以得出△ECH为等腰直角三角形,从而得出结论.
解答:解:(1)ME=MC,ME⊥MC
理由:如图1,延长EM、AD交于点H,连接EC,HC,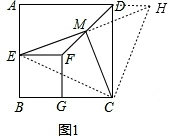
∵四边形ABCD和四边形EBGF都是正方形,
∴BC=CD,∠A=∠B=∠BCD=∠ADC=∠BEF=90°,EF=EB.
∴AD∥EF,
∴∠EFM=∠HDM,∠FEM=∠DHM.∠BCD=∠CDH.
∴∠B=∠CDH.
∵点M是线段DF的中点,
∴FM=DM.
在△EFM和△HDM中
,
∴△EFM≌△HDM(AAS),
∴EF=DH.EM=HM.
∴BE=DH.
在△EBC和△HDC中
∴△EBC≌△HDC(SAS),
∴EC=HC,∠ECB=∠HCD.
∵∠BCE+∠ECD=90°,
∴∠HCD+∠ECD=90°,
∴∠ECH=90°.
∴∠MEC=45°.
∵EM=HM,EC=HC,
∴EM⊥CM,∠ECM=45°,
∴∠MEC=∠MCE
∴EM=MC;
(2)ME=MC,ME⊥MC
理由:延长EM到H.使MH=ME,连接DH,EC,HC,
∵点M是线段DF的中点,
∴FM=DM.
在△EFM和△HDM中
,
∴△EFM≌△HDM(SAS),
∴EF=DH.
正方形EBGF绕点B顺时针旋转α度,
∴∠ABE=∠NDH=a.
∵四边形ABCD和四边形EBGF都是正方形,
∴BC=CD,∠A=∠B=∠BCD=∠ADC=∠BEF=90°,EF=EB.AD∥BC,
∴∠NDC=∠BCD=90°.EB=DH.
∴∠ABC=∠NDC,
∴∠ABC-∠ABF=∠NDC-NDH,
∴∠EBC=∠HDC
在△EBC和△HDC中
∴△EBC≌△HDC(SAS),
∴EC=HC,∠ECB=∠HCD.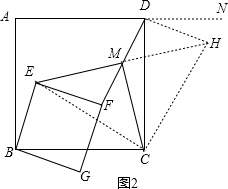
∵∠BCE+∠ECD=90°,
∴∠HCD+∠ECD=90°,
∴∠ECH=90°.
∴∠MEC=45°.
∵EM=HM,EC=HC,
∴EM⊥CM,∠ECM=45°,
∴∠MEC=∠MCE
∴EM=MC.
理由:如图1,延长EM、AD交于点H,连接EC,HC,

∵四边形ABCD和四边形EBGF都是正方形,
∴BC=CD,∠A=∠B=∠BCD=∠ADC=∠BEF=90°,EF=EB.
∴AD∥EF,
∴∠EFM=∠HDM,∠FEM=∠DHM.∠BCD=∠CDH.
∴∠B=∠CDH.
∵点M是线段DF的中点,
∴FM=DM.
在△EFM和△HDM中
|
∴△EFM≌△HDM(AAS),
∴EF=DH.EM=HM.
∴BE=DH.
在△EBC和△HDC中
|
∴△EBC≌△HDC(SAS),
∴EC=HC,∠ECB=∠HCD.
∵∠BCE+∠ECD=90°,
∴∠HCD+∠ECD=90°,
∴∠ECH=90°.
∴∠MEC=45°.
∵EM=HM,EC=HC,
∴EM⊥CM,∠ECM=45°,
∴∠MEC=∠MCE
∴EM=MC;
(2)ME=MC,ME⊥MC
理由:延长EM到H.使MH=ME,连接DH,EC,HC,
∵点M是线段DF的中点,
∴FM=DM.
在△EFM和△HDM中
|
∴△EFM≌△HDM(SAS),
∴EF=DH.
正方形EBGF绕点B顺时针旋转α度,
∴∠ABE=∠NDH=a.
∵四边形ABCD和四边形EBGF都是正方形,
∴BC=CD,∠A=∠B=∠BCD=∠ADC=∠BEF=90°,EF=EB.AD∥BC,
∴∠NDC=∠BCD=90°.EB=DH.
∴∠ABC=∠NDC,
∴∠ABC-∠ABF=∠NDC-NDH,
∴∠EBC=∠HDC
在△EBC和△HDC中
|
∴△EBC≌△HDC(SAS),
∴EC=HC,∠ECB=∠HCD.

∵∠BCE+∠ECD=90°,
∴∠HCD+∠ECD=90°,
∴∠ECH=90°.
∴∠MEC=45°.
∵EM=HM,EC=HC,
∴EM⊥CM,∠ECM=45°,
∴∠MEC=∠MCE
∴EM=MC.
点评:本题考查了正方形的性质的运用,旋转的性质的运用,全等三角形的判定及性质的运用,等腰直角三角形的判定及性质的运用,解答时证明三角形全等是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
二次函数y=x2+3的图象向右平移3个单位,得到新的图象的函数解析式是( )
| A、y=x2 |
| B、y=(x+3)2 |
| C、y=(x-3)2 |
| D、y=(x-3)2+3 |
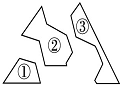 如图,某同学把一块三角形状的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样
如图,某同学把一块三角形状的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的方法是带③去,依据是三角形的全等判定( )
| A、SAS | B、ASA |
| C、SSS | D、AAS |
下列说法中正确的是( )
| A、1是单项式 |
| B、单项式m的系数为0,次数为0 |
| C、单项式2a2b的系数是2,次数是2 |
| D、xy-x+y-4的项是xy,x,y,4 |

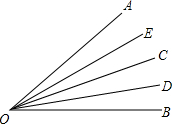 已知:如图,∠AOB=40°,OC平分∠AOB,OD、OE分别平分∠BOC和∠AOC.
已知:如图,∠AOB=40°,OC平分∠AOB,OD、OE分别平分∠BOC和∠AOC.