题目内容
17．化简求值：$\frac{2a}{{a}^{2}-4}$÷（$\frac{{a}^{2}}{a-2}$-a），其中a=$\sqrt{3}$-2．分析 先根据分式混合运算的法则把原式进行化简，再把a的值代入进行计算即可．
解答 解：原式=$\frac{2a}{（a+2）（a-2）}$÷$\frac{2a}{a-2}$
=$\frac{2a}{（a+2）（a-2）}$•$\frac{a-2}{2a}$
=$\frac{1}{a+2}$，
当a=$\sqrt{3}$-2时，原式=$\frac{1}{\sqrt{3}-2+2}$=$\frac{\sqrt{3}}{3}$．
点评 本题考查的是分式的化简求值，熟知分式混合运算的法则是解答此题的关键．
练习册系列答案
相关题目
7．2015年5月17日是第25个全国助残日，今年全国助残日的主题是“关注孤独症儿童，走向美好未来”．第二次全国残疾人抽样调查结果显示，我国0～6岁精神残疾儿童约为11.1万人．11.1万用科学记数法表示为（ ）
| A． | 1.11×104 | B． | 11.1×104 | C． | 1.11×105 | D． | 1.11×106 |
8．
如图，在四边形ABCD中，AB=CD，BA和CD的延长线交于点E，若点P使得S△PAB=S△PCD，则满足此条件的点P（ ）
如图，在四边形ABCD中，AB=CD，BA和CD的延长线交于点E，若点P使得S△PAB=S△PCD，则满足此条件的点P（ ）| A． | 有且只有1个 | |
| B． | 有且只有2个 | |
| C． | 组成∠E的角平分线 | |
| D． | 组成∠E的角平分线所在的直线（E点除外） |
5．
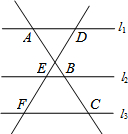如图，l1∥l2∥l3，两条直线与这三条平行线分别交于点A、B、C和D、E、F．已知$\frac{AB}{BC}=\frac{3}{2}$，则$\frac{DE}{DF}$的值为（ ）
如图，l1∥l2∥l3，两条直线与这三条平行线分别交于点A、B、C和D、E、F．已知$\frac{AB}{BC}=\frac{3}{2}$，则$\frac{DE}{DF}$的值为（ ）| A． | $\frac{3}{2}$ | B． | $\frac{2}{3}$ | C． | $\frac{2}{5}$ | D． | $\frac{3}{5}$ |
如图，在等腰三角形ABC中，AB=AC，DE垂直平分AB，已知∠ADE=40°，则∠DBC=15°．
6．已知一个表面积为12dm2的正方体，则这个正方体的棱长为（ ）
| A． | 1dm | B． | $\sqrt{2}$dm | C． | $\sqrt{6}$dm | D． | 3dm |